9장 계산복잡도와 다루기 난이도: NP 이론 소개

주요 내용

• 1절 계산복잡도와 다루기 난이도

• 3절 다루기 난이도 분류

• 4절 NP 이론

1절 계산복잡도와 다루기 난이도

계산복잡도(computational complexity)

• 계산복잡도 연구: 주어진 문제를 풀 수 있는 가능한 모든 알고리즘에 대한 연구

• 계산복잡도 분석: 같은 문제를 푸는 모든 알고리즘의 효율설(복잡도)의 하한 구하기

예제: 행렬곱셈 문제

• 행렬곱셈 문제를 푸는 하한(lower bound): $\Omega(n^2)$

• 지금까지 알려진 최고 성능 알고리즘
  • Le Gall (2014)
  • $\Theta(n^{2.3728639})$

하한의 의미

• 행렬 곱셈을 실행하는 어떤 알고리즘도 $\Theta(n^2)$ 보다 좋을 수는 없음.

• 하지만 $\Theta(n^2)$의 복잡도를 갖는 알고리즘을 찾을 수 있다는 것을 보장하지는 않음.

예제: 정렬 문제

• 알려진 하한 만큼 좋은 알고리즘 존재

• 정렬 문제의 하한: $\Omega(n \lg n)$

다루기 난이도(Intractability)

다차시간 알고리즘(polynomial-time algorithm)

• 최악 시간복잡도의 상한이 다항식인 알고리즘

  $$ W(n) \in O(p(n)) $$

  여기서, $p(n)$은 다항식.

• 최악 시간복잡도가 아래와 같은 알고리즘은 모두 다차시간 알고리즘임:

  $$ 2n \qquad 3 n^3 + 4n \qquad 5n+n^{10} \qquad n \lg n $$

• 주의: $n\lg n < n^2$

• 최악 시간복잡도가 아래와 같은 알고리즘은 모두 다차시간 알고리즘 아님:

  $$ 2^n \qquad 2^{0.01 n} \qquad 2^{\sqrt{n}} \qquad n! $$

• 비다차시간 알고리즘도 경우에 따라 효율적으로 실행되는 사례가 많음.
  • 예제: 되추적 알고리즘

• 반대로 경우에 따라 다차시간 알고리즘이 있는 문제가 그렇지 않은 문제보다 실제 상황에서 더 어려운 경우 있음.

• 따라서 다루기 난이도를 실제로 다루기 힘들 수 있다는 정도로만 해석할 필요 있음.

3절 문제 분류

1) 다차시간 알고리즘을 찾은 문제

2) 다루기 힘들다고 증명된 문제

3) 다루기 힘들다고 증명되지 않았지만 다차시간 알고리즘도 찾지 못한 문제

다차시간 알고리즘을 찾은 문제

• 다차시간 알고리즘이 알려진 문제

• 예제: 정렬된 배열검색, $\Theta(\lg n)$

• 예제: 행렬 곱셈, $\Theta(n^{2.3728639})$

다루기 힘들다고 증명된 문제

• 두 종류로 분류됨
  • 지수 이상의 출력을 요구하는 문제: 예를 들어 모든 경로를 다 출력하는 문제
  • 지수 이상의 출력을 요구하지 않지만 문제를 다차시간 내에 풀 수 없음이 증명된 문제
    • 예제: 정지문제(Halting problem) 등 진위판별문제 관련 문제 다수 존재

다루기 힘들다고 증명되지 않았지만 다차시간 알고리즘도 찾지 못한 문제

• 다차시간 알고리즘이 알려지지 않았지만 그렇다고 해서 다차시간 알고리즘이 존재하지 않는다는 증명도 없는 문제

• 다수 존재. 지금까지 알려진 다루기 어려운 문제의 대다수가 이런 문제임
  • 예제: 0-1 배낭채우기 문제, 외판원 문제, m-색칠하기 문제(m > 2) 등등

NP 이론

• 다차시간 알고리즘 문제와 비다차시간 알고리즘을 분류하는 기준에 대한 이론

P 와 NP

집합 P

• 다차시간 알고리즘으로 풀 수 있는 모든 진위판별 문제의 집합

• 예제: 특정 항목이 주어진 배열에 포함되었는지 여부 판단하는 문제

• 외판원 특정 시간 안에 모든 도시를 방문하고 돌아올 수 있는지를 판멸하는 문제
  • 이 문제에 대해 다차시간 알고리즘이 알려지지 않았으며, 그리고 그런 다차시간 알고리즘이 존재하지 않는다는 증명도 아직 없음.

집합 NP

• NP: 다차시간 비결정 알고리즘 풀 수 있는 모든 진위판별 문제들의 집합
  • NP = nondeterministical polynomial

• 다차시간 비결정 알고리즘: 검증단계가 다차시간 알고리즘인 비결정 알고리즘

• 비결정 알고리즘 작동법
  • (비결정) 추측 단계: 문제의 답을 임의로 추측하여 생성
  • (결정) 검증 단계: 임의로 추측된 답의 참/거짓 여부 판단

P 이면 NP!

• P 에 속하는 문제는 모두 NP에도 속한다.

축소변환 가능성

• 진위판별 문제 A를 진위판별 문제 B로 변환하는 다차시간 변환 알고리즘이 존해할 때 문제 A는 문제 B로 다차시간 다일 축소변환가능(polynomial-time many-one reducible)이다라고 함.

• 간단하게 축소변환 가능이라 말하며 아래와 같이 표시함:

  $$A \propto B$$

NP-complete 문제

• 아래 두 조건을 만족하는 문제 B를 NP-complete 라 함.
  1. NP에 속함.
  2. NP에 속한 임의의 다른 문제 A를 다차시간 내에 B의 문제로 축소변환 가능함.

• 예제: 외판원 문제, 0-1 배낭채우기 등등 지금까지 알려진 다루기 어려운 문제 대다수

NP-hard 문제

• 최소 NP-complete 만큼 다루기 어려운 문제

P, NP, NP-complete, NP-hard 의 현재 상태

• 주의: 아직 P = NP 여부 모름

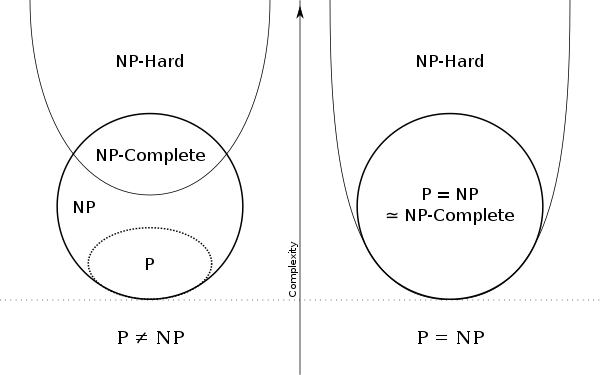
<그림 출처: 위키피디아: P versus NP problem>