5장 되추적¶
주요 내용¶
- 1절 되추적 기법
- 2절 n-퀸 문제
- 5절 그래프 색칠하기
- 부록: 제네릭 프로그래밍 활용
1절 제약충족 문제와 되추적 기법¶
제약충족 문제(CSP, constraint-satisfaction problems)¶
- 특정 변수에 할당할 값을 지정된 도메인(영역, 집합)에서 정해진 조건에 따라 선택하는 문제
- 예제: 4-퀸 문제(체스 퀸(queen) 네 개의 위치 선정하기)
- 변수: 네 개의 퀸
- 즉, 1번 퀸부터 4번 퀸.
- 도메인: {1, 2, 3, 4}
- 즉, 1번 열부터 4번 열.
- 조건: 두 개의 퀸이 하나의 행, 열, 또는 대각선 상에 위치하지 않음.
- 변수: 네 개의 퀸

되추적 기법(백트래킹, backtracking)¶
- 제약충족 문제를 해결하는 일반적인 기법
- 문제에 따라 다른 제약충족 조건만 다를 뿐 문제해결을 위한 알고리즘은 동일함.
- 여기서는 두 개의 문제를 이용하여 되추적 기법의 활용법을 설명함.
주요 기초개념¶
- 깊이우선 탐색
- 상태 공간 나무
- 마디의 유망성
- 가지치기
깊이우선 탐색¶
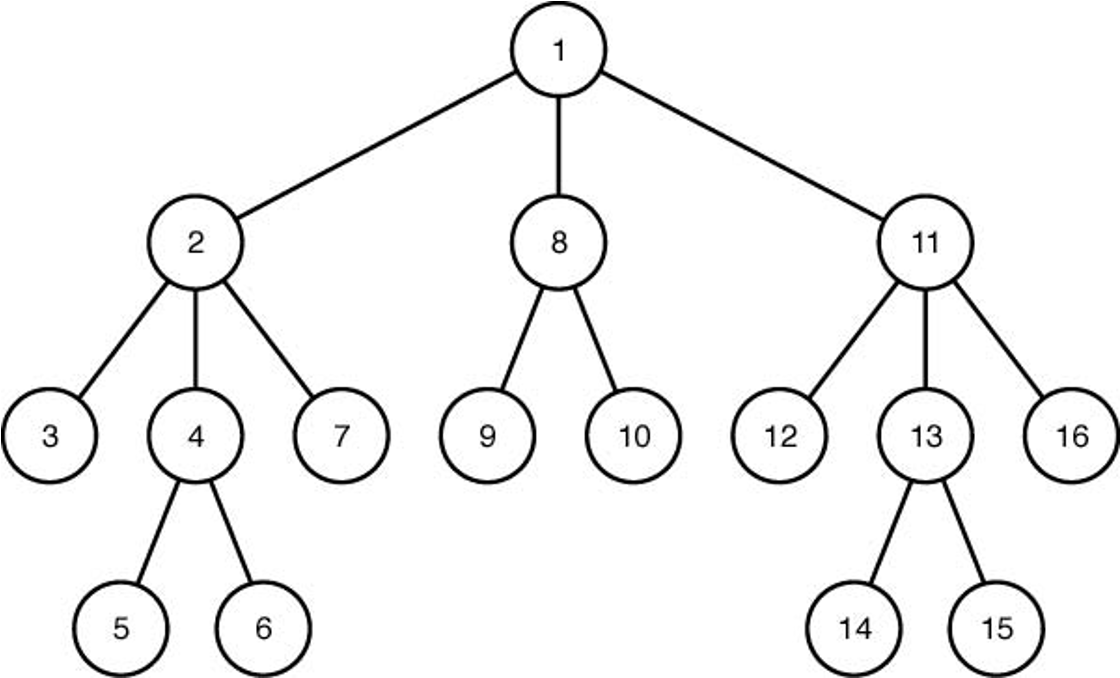
- DFS(depth-first-search): 뿌리 지정 나무(rooted tree)를 대상으로 하는 탐색기법.
- 왼편으로 끝(잎마디)까지 탐색한 후에 오른편 형제자매 마디로 이동
- 예제:
- 아래 뿌리 지정 나무의 뿌리에서 출발하여 왼편 아랫쪽 방향으로 진행.
- 더 이상 아래 방향으로 진행할 수 없으면 부모 마디로 돌아간 후 다른 형제자매 마디 중 가장 왼편에 위치한 마디로 이동 후 왼편 아랫쪽 방향으로의 이동 반복
상태 공간 나무(state space tree)¶
- 변수가 가질 수 있는 모든 값을 마디(node)로 갖는 뿌리 지정 나무
- 깊이: 깊이가 0인 뿌리에서 출발하여 아래로 내려갈 수록 깊이가 1씩 증가.
- 예제:
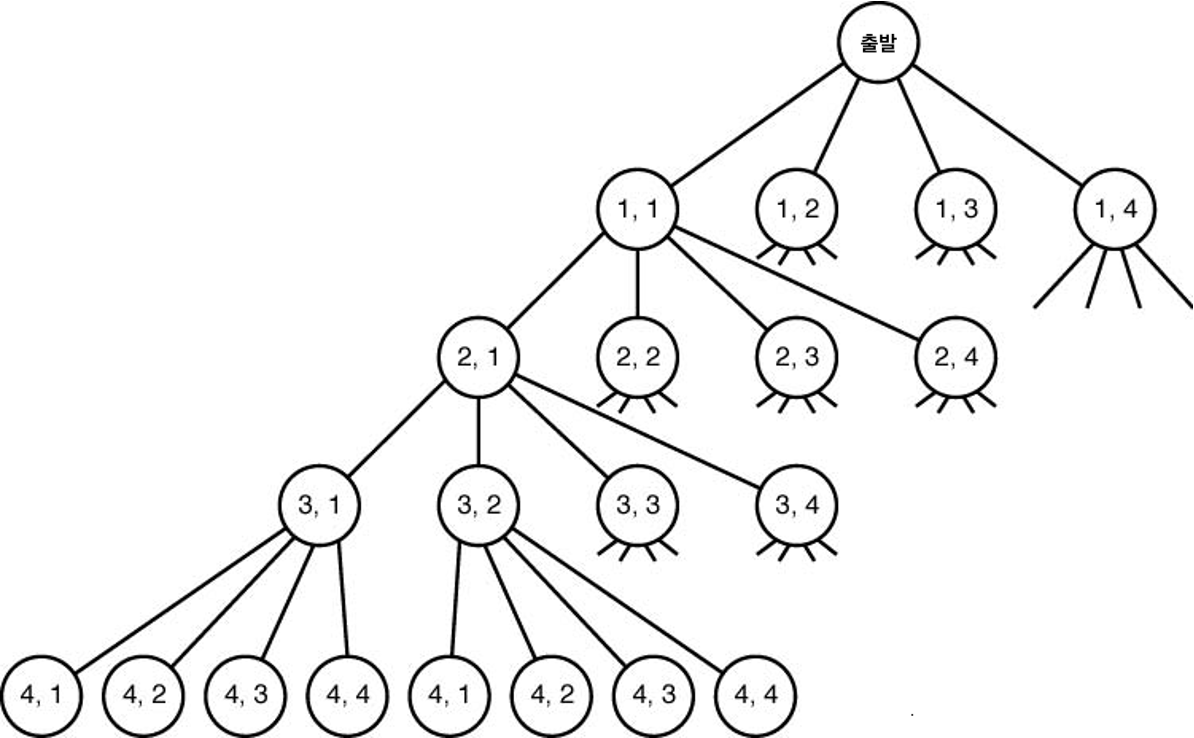
4x4로 이루어진 체스판에 네 개의 체스 퀸을 놓을 수 있는 위치를 마디로 표현한 상태 공간 나무- 뿌리는 출발 마디로 표현하며, 체스 퀸의 위치와 상관 없음.
- 깊이 $k$의 마디: $k$ 째 퀸이 놓일 수 있는 위치
마디의 유망성¶
- 지정된 특정 조건에 해당하는 마디를 유망하다라고 부름.
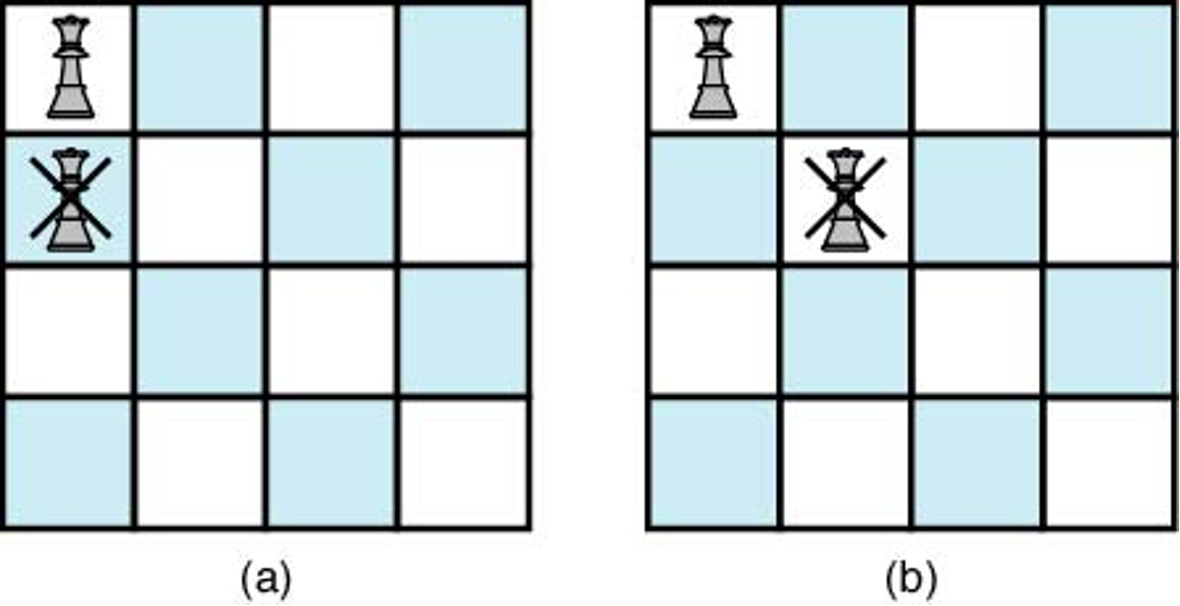
- 예제: 네 개의 퀸을 위치시켜야 할 경우 첫째 퀸의 위치에 따라
둘째 퀸이 놓일 수 있는 위치의 유망성이 결정됨.
- 아래 그림에서 2번 행의 1, 2번 칸은 유망하지 않음.
가지치기(pruning)¶
- 특정 마디에서 시작되는 가지 제거하기
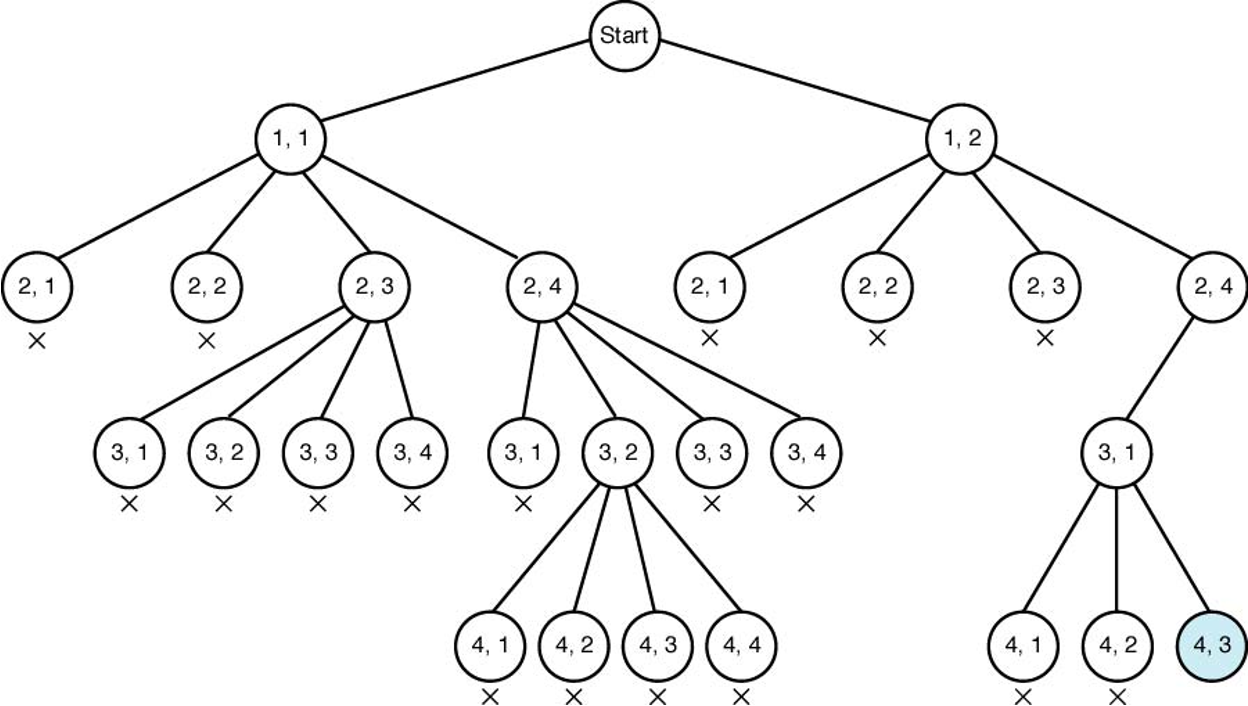
- 예제: 4 x 4로 이루어진 체스판에 네 개의 체스 퀸을 놓을 수 있는 위치를 마디로 표현한 상태 공간 나무에서 유망하지 않은 마디에서 가지치기를 실행하면 아래 그림이 생성됨.
되추적 알고리즘¶
상태 공간 나무의 뿌리로부터 깊이우선 탐색(DFS) 실행.
탐색 과정에서 유망하지 않은 마디를 만나면 가지치기 실행 후 부모 마디로 되돌아감(되추적, backtracking).
이후 다른 형제자매 마디를 대상으로 깊이우선 탐색 반복. 더 이상의 형제자매 마디가 없으면 형제자매가 있는 조상까지 되추적 실행.
탐색이 더 이상 진행할 수 없는 경우 알고리즘 종료
예제: 되추적 알고리즘을 활용한 4-퀸 문제 해결¶
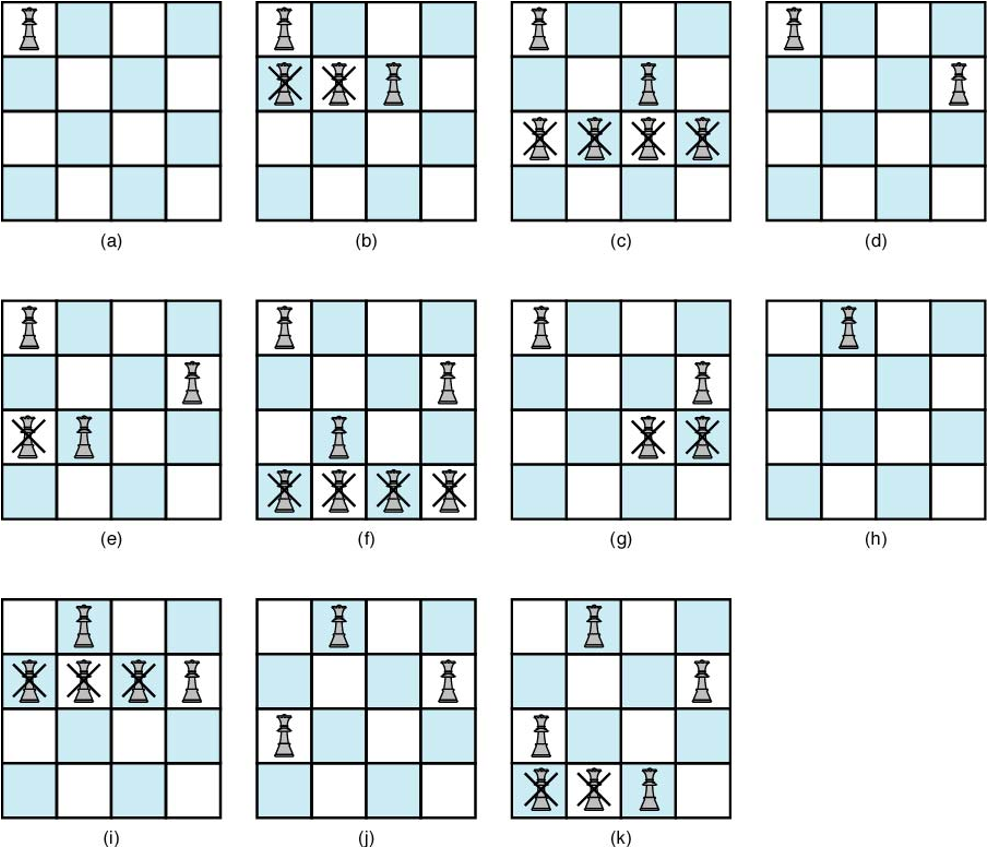
깊이우선 탐색 대 되추적 알고리즘 비교¶
- 4-퀸 문제를 순수한 깊이우선 탐색으로 해결하고자 할 경우: 155 마디 검색
- 4-퀸 문제를 되추적 알고리즘으로 해결하고자 하는 경우: 27 마디 검색
2절 n-퀸 문제¶
- 4-퀸 문제를 일반화시킨 n-문제를 해결하는 되추적 알고리즘 구현하기
문제: n 개의 퀸(queen)을 서로 상대방을 위협하지 않도록 n x n 체스판에 위치시키기
변수: n 개의 퀸
- 즉, 1번 퀸부터 n번 퀸.
- 즉, 1번 퀸부터 n번 퀸.
도메인: {1, 2, ..., n}
- 즉, 1번 열부터 n번 열.
- 즉, 1번 열부터 n번 열.
조건: 두 개의 퀸이 하나의 행, 열, 또는 대각선 상에 위치하지 않음.
유망성 판단¶
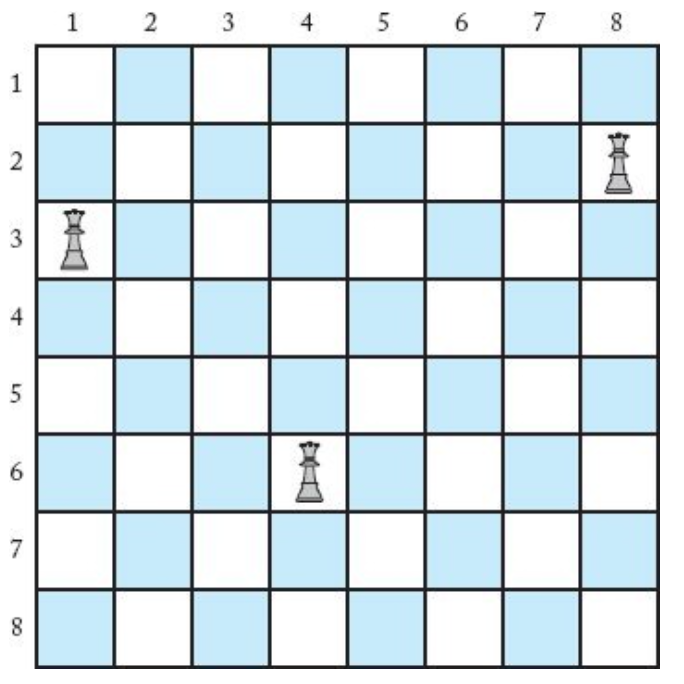
두 개의 퀸 $q_1, q_2$가 같은 대각선 상에 위치하려면 행과 열의 차이의 절댓값이 동일해야 함. (아래 그림 참조)
$$ \text{abs}(q_{1,r} - q_{2,r}) = \text{abs}(q_{1,c} - q_{2,c}) $$
단, $(q_{1,r}, q_{1,c})$ 와 $(q_{2,r}, q_{2,c})$ 는 각각 $q_1$과 $q_2$가 위치한 행과 열의 좌표를 가리킴.
예제: 4-퀸 문제 해결 되추적 알고리즘¶
from typing import List, Dict
# 변수: 네 개의 퀸의 번호, 즉, 1, 2, 3, 4
variables = [1, 2, 3, 4]
# 도메인: 각각의 퀸이 자리잡을 수 있는 가능한 모든 열의 위치.
domains: Dict[int, List[int]] = {}
columns = [1, 2, 3, 4]
for var in variables:
domains[var] = columns
- 4-퀸 문제의 경우 각각의 퀸 모두 동일하게 1열부터 4열 어딘가에 위치할 수 있음. 단, 그 중에서 조건을 만족시키는 열을 찾아야 함.
domains
{1: [1, 2, 3, 4], 2: [1, 2, 3, 4], 3: [1, 2, 3, 4], 4: [1, 2, 3, 4]}
되추적 함수 구현¶
- 아래 되추적 함수
backtracking_search_queens()는 일반적인 n-퀸 문제를 해결함.assignment인자: 되추적 과정에서 일부의 변수에 대해 할당된 도메인 값의 정보를 담은 사전을 가리킴.- 인자가 들어오면 아직 값을 할당받지 못한 변수를 대상으로 유망성을 확인한 후 되추적 알고리즘 진행.
- 되추적 알고리즘이 진행되면서
assignment가 확장되며 모든 변수에 대해 도메인 값이 지정될 때가지 재귀적으로 알고리즘이 진행됨.
def backtracking_search_queens(assignment: Dict[int, int] = {}):
"""assignment: 각각의 변수를 키로 사용하고 키값은 해당 변수에 할당될 값"""
# 모든 변수에 대한 값이 지정된 경우 조건을 만족시키는 해가 완성된 것임
if len(assignment) == len(variables):
return assignment
# 아직 값을 갖지 않은 변수들이 존재하면 되추적 알고리즘을 아직 할당되지 않은 값을 대상으로 이어서 진행
unassigned = [v for v in variables if v not in assignment]
first = unassigned[0]
for value in domains[first]:
# 주의: 기존의 assignment를 보호하기 위해 복사본 활용
# 되추적이 발생할 때 이전 할당값을 기억해 두기 위해서임.
local_assignment = assignment.copy()
local_assignment[first] = value
# local_assignment 값이 유망하면 재귀 호출을 사용하여 변수 할당 이어감.
if promissing_queens(first, local_assignment):
result = backtracking_search_queens(local_assignment)
# 유망성을 이어가지 못하면 되추적 실행
if result is not None:
return result
return None
유망성 확인 함수¶
def promissing_queens(variable: int, assignment: Dict[int, int]):
"""새로운 변수 variable에 값을 할당 하면서 해당 변수와 연관된 변수들 사이의 제약조건이
assignment에 대해 만족되는지 여부 확인
n-퀸 문제의 경우: 제약조건이 모든 변수에 대해 일정함.
즉, 새로 위치시켜야 하는 퀸이 기존에 이미 자리잡은 퀸들 중 하나와
동일 행, 열, 대각산 상에 위치하는지 여부를 확인함"""
# q1r, q1c: 첫째 퀸이 놓인 마디의 열과 행
for q1r, q1c in assignment.items():
# q2r = 첫째 퀸 아래에 위치한 다른 모든 퀸들을 대상으로 조건만족여부 확인
for q2r in range(q1r + 1, len(assignment) + 1):
q2c = assignment[q2r] # 둘째 퀸의 열
if q1c == q2c: # 동일 열에 위치?
return False
if abs(q1r - q2r) == abs(q1c - q2c): # 대각선상에 위치?
return False
# 모든 변수에 대해 제약조건 만족됨
return True
backtracking_search_queens()
{1: 2, 2: 4, 3: 1, 4: 3}
n-퀸 문제 되추적 알고리즘의 시간 복잡도¶
n 개의 퀸이 주어졌을 때 상태공간트리의 마디의 수는 다음과 같음.
$$ 1 + n + n^2 + n^3 + \cdots + n^n = \frac{n^{n+1}-1}{n-1} $$
- 따라서 되추적 알고리즘이 최대 n의 지수승 만큼 많은 수의 마디를 검색해야 할 수도 있음.
- 하지만 검색해야 하는 마디 수는 경우마다 다름.
- 효율적인 알고리즘이 아직 알려지지 않음.
부록: 얕은(shallow) 복사 vs 깊은(deep) 복사¶
- 리스트의
copy()메서드는 얕은 복사 용도로 사용된.- 1차원 리스트일 경우 새로운 리스트를 복사해서 만들어 냄.
- 하지만 2차원 이상의 리스트 일 경우 모든 것을 복사하지는 않음. 아래 코드 참조.
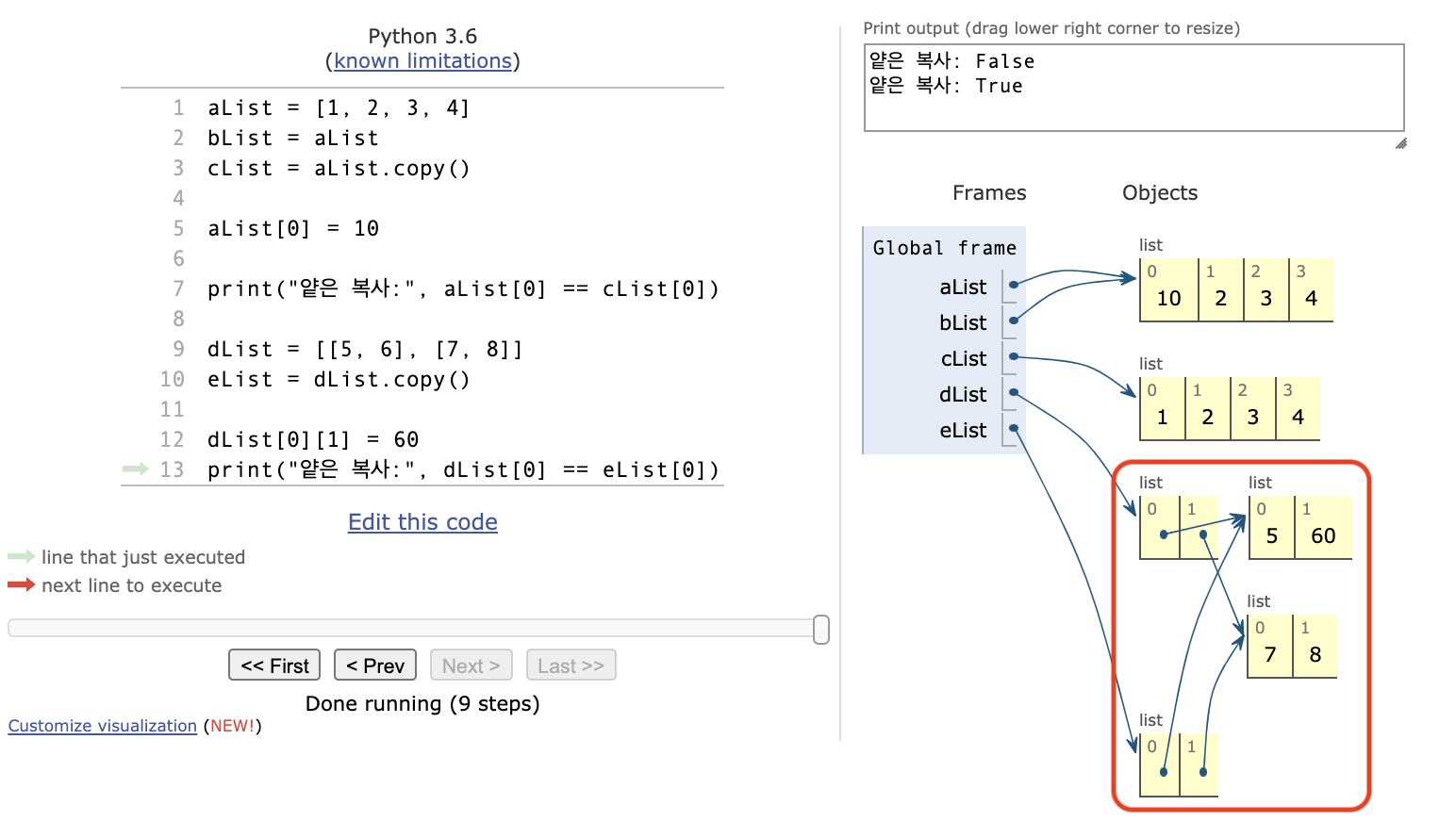
# 얕은 복사
aList = [1, 2, 3, 4]
bList = aList
cList = aList.copy()
aList[0] = 10
print("얕은 복사:", aList[0] == cList[0])
dList = [[5, 6], [7, 8]]
eList = dList.copy()
dList[0][1] = 60
print("얕은 복사:", dList[0] == eList[0])
얕은 복사: False 얕은 복사: True
- 깊은 차원까지 복사를 하려면 깊은 복사(deep copy)를 사용해야 함.
- 방식1: 새로 정의
- 방식2:
copy모듈의deepcopy()함수 활용copy()함수: 얕은 복사. 리스트의copy()메서드와 동일하게 작동.deepcopy()함수: 깊은 복사.
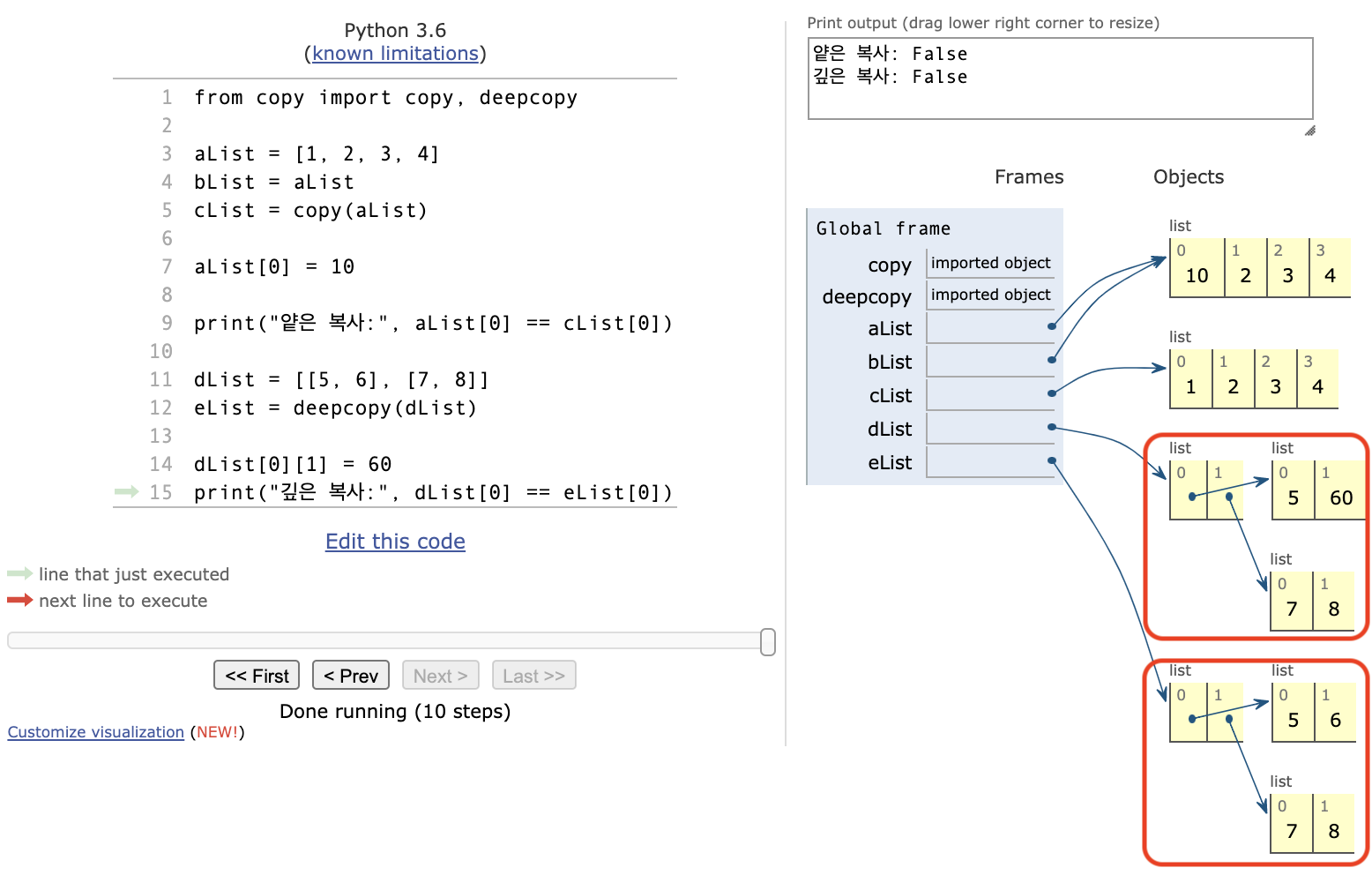
# 얕은 복사 vs. 얕은 복사
from copy import copy, deepcopy
aList = [1, 2, 3, 4]
bList = aList
cList = copy(aList)
aList[0] = 10
print("얕은 복사:", aList[0] == cList[0])
dList = [[5, 6], [7, 8]]
eList = deepcopy(dList)
dList[0][1] = 60
print("깊은 복사:", dList[0] == eList[0])
얕은 복사: False 깊은 복사: False
5절 그래프 색칠하기¶
m-색칠하기¶
- 주어진 비방향그래프에서 서로 인접한 마디를 최대 m 개의 색상을 이용하여 서로 다른 색을 갖도록 색칠하는 문제
예제¶
- 아래 그래프에 대한 2-색칠하기 문제의 해답은 없음.
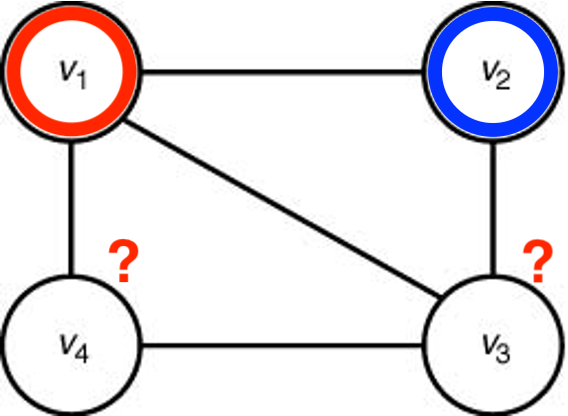
- 3-색칠하기 문제에 대해서는 해답 존재.
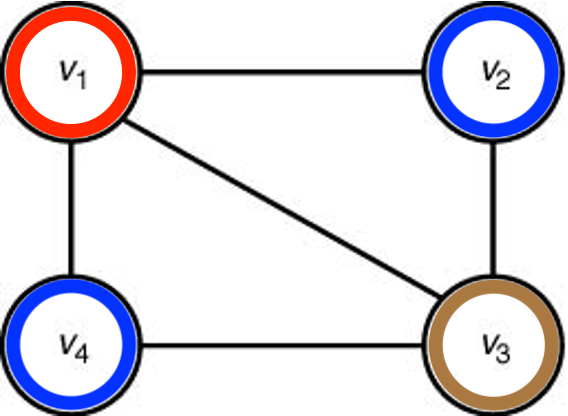
주요 응용분야¶
- 지도 색칠하기
평면그래프¶
- 서로 교차하는 이음선이 없는 그래프
- 지도를 평면그래프로 변환 가능
- 마디: 지도의 한 지역
- 이음선: 서로 인접한 두 지역 연결
예제¶
- 왼편의 지도를 오른편의 평면그래프로 변환 가능함.
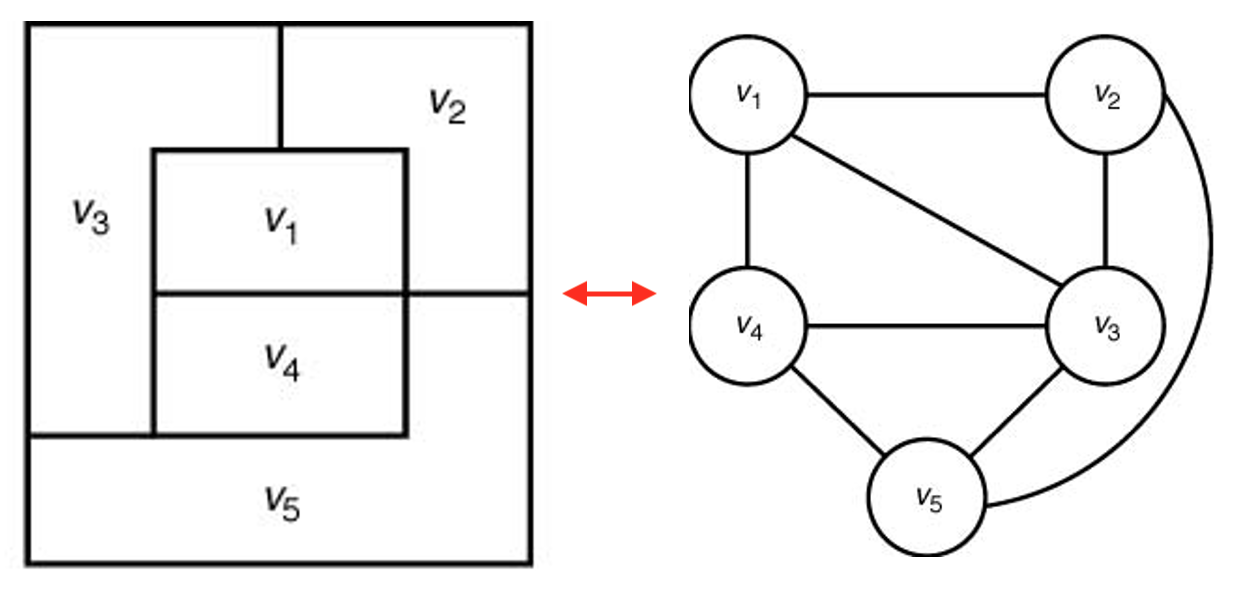
예제: 3-색칠하기 문제 해결 되추적 알고리즘¶
colors = [빨강, 파랑, 갈색]
= [1 , 2 , 3 ]

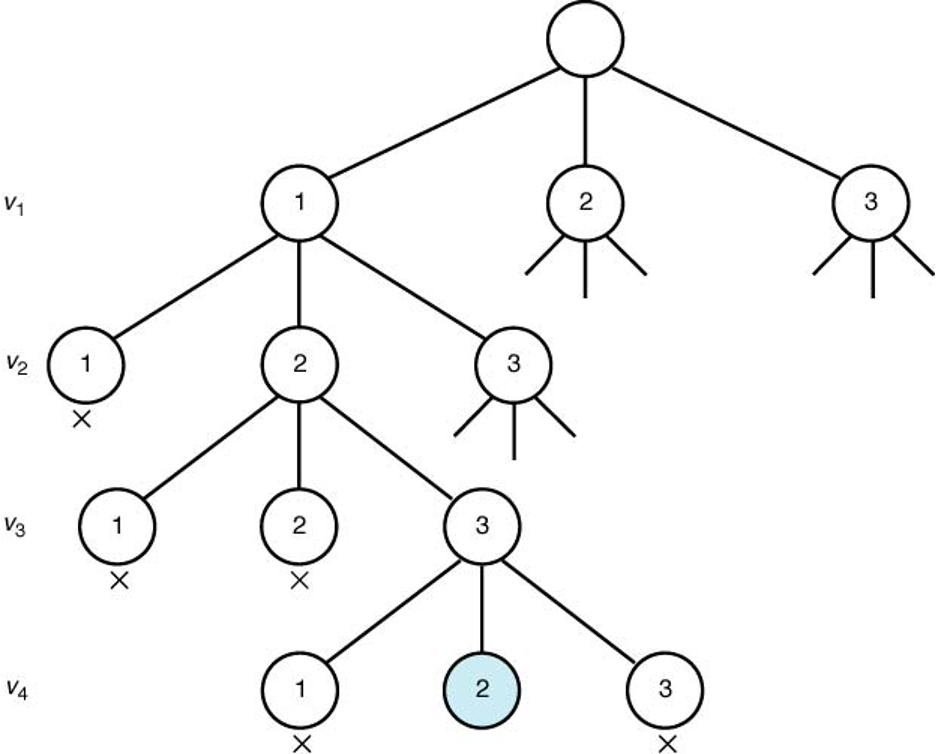
from typing import List, Dict
# 변수: 네 마디의 번호, 즉, 1, 2, 3, 4
variables = [1, 2, 3, 4]
# 도메인: 각각의 마디에 칠할 수 있는 가능한 모든 색상
# 3-색칠하기: 1(빨강), 2(파랑), 3(갈색)
domains: Dict[int, List[int]] = {}
columns = [1, 2, 3]
for var in variables:
domains[var] = columns
- 3-색칠하기 문제의 경우 각각의 마디에 동일하게 빨강, 파랑, 갈색 어느 색도 취할 수 있음. 단, 그 중에서 조건을 만족시키는 색상을 찾아야 함.
domains
{1: [1, 2, 3], 2: [1, 2, 3], 3: [1, 2, 3], 4: [1, 2, 3]}
되추적 함수 구현¶
- 아래 되추적 함수
backtracking_search_colors()는 일반적인 m-색칠하기 문제를 해결함.assignment인자: 되추적 과정에서 일부의 변수에 대해 할당된 도메인 값의 정보를 담은 사전을 가리킴.- 인자가 들어오면 아직 값을 할당받지 못한 변수를 대상으로 유망성을 확인한 후 되추적 알고리즘 진행.
- 되추적 알고리즘이 진행되면서
assignment가 확장되며 모든 변수에 대해 도메인 값이 지정될 때가지 재귀적으로 알고리즘이 진행됨.
def backtracking_search_colors(assignment: Dict[int, int] = {}):
"""assignment: 각각의 변수를 키로 사용하고 키값은 해당 변수에 할당될 값"""
# 모든 변수에 대한 값이 지정된 경우 조건을 만족시키는 해가 완성된 것임
if len(assignment) == len(variables):
return assignment
# 아직 값을 갖지 않은 변수들이 존재하면 되추적 알고리즘을 아직 할당되지 않은 값을 대상으로 이어서 진행
unassigned = [v for v in variables if v not in assignment]
first = unassigned[0]
for value in domains[first]:
# 주의: 기존의 assignment를 보호하기 위해 복사본 활용
# 되추적이 발생할 때 이전 할당값을 기억해 두기 위해서임.
local_assignment = assignment.copy()
local_assignment[first] = value
# local_assignment 값이 유망하면 재귀 호출을 사용하여 변수 할당 이어감.
if promissing_colors(first, local_assignment):
result = backtracking_search_colors(local_assignment)
# 유망성을 이어가지 못하면 되추적 실행
if result is not None:
return result
return None
유망성 확인 함수¶
def promissing_colors(variable: int, assignment: Dict[int, int]):
"""새로운 변수 variable에 값을 할당 하면서 해당 변수와 연관된 변수들 사이의 제약조건이
assignment에 대해 만족되는지 여부 확인
m-색칠하기 문제의 경우: 이웃마디의 상태에 따라 제약조건이 달라짐.
즉, 마디 variable에 할당된 색이 이웃마디의 색과 달라야 함.
이를 위해 각각의 마디가 갖는 이웃마디들의 리스트를 먼저 확인해야 함."""
# 각 마디에 대한 이웃마디의 리스트
constraints = {
1 : [2, 3, 4],
2 : [1, 3],
3 : [1, 2, 4],
4 : [1, 3]
}
for var in constraints[variable]:
if (var in assignment) and (assignment[var] == assignment[variable]):
return False
return True
backtracking_search_colors()
{1: 1, 2: 2, 3: 3, 4: 2}
m-색칠하기 문제 되추적 알고리즘의 시간 복잡도¶
n 개의 마디를 m 개의 색으로 칠해야 하는 문제의 상태공간트리의 마디의 수는 다음과 같음.
$$ 1 + m + m^2 + m^3 + \cdots + m^n = \frac{m^{n+1}-1}{m-1} $$
- 따라서 되추적 알고리즘이 최대 m과 n의 지승 만큼 많은 수의 마디를 검색해야 할 수도 있음.
- 하지만 검색해야 하는 마디 수는 경우마다 다름.
- 효율적인 알고리즘이 아직 알려지지 않음.
참고: 4색정리¶
- 4-색칠하기 문제는 언제나 해결가능함.
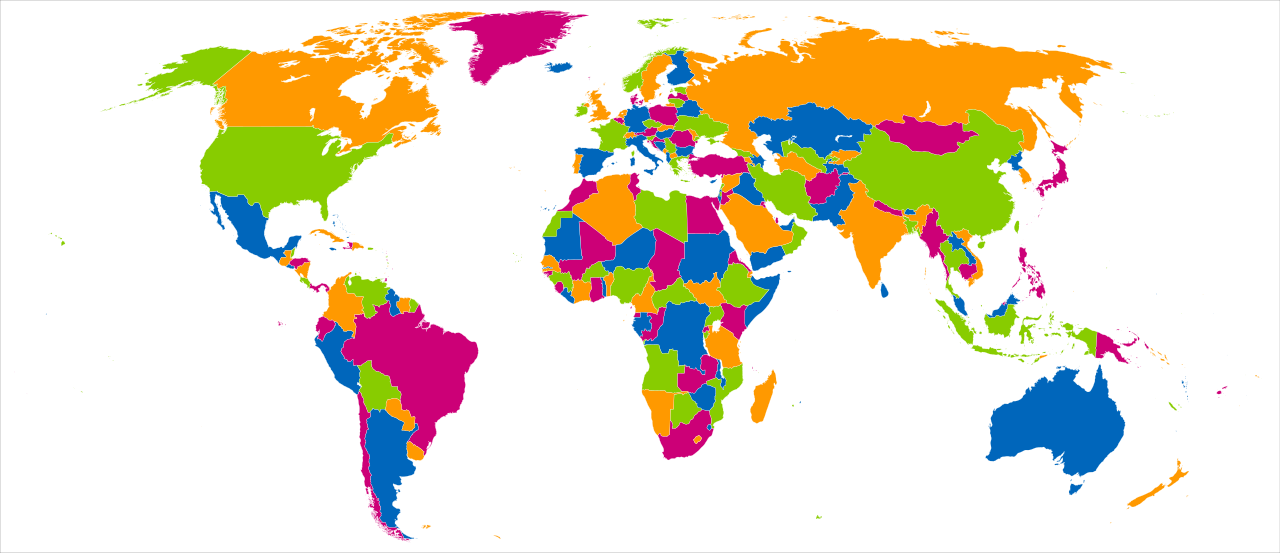
<그림 출처: 위키피디아: 4색정리>
- 1852년에 영국인 Francis Guthrie가 영국 지도를 작성할 때 인접한 각 주를 다른 색으로 칠하기 위해 필요한 최소한의 색상의 수에 대한 질문에서 유래한 문제임.
- 해결
- 1976년에 K. Appel과 W. Haken 이 해결
- 500페이지 이상의 증명으로 이루어졌으며 일부 증명은 컴퓨터 프로그램을 사용하였음.
- 증명에 사용된 컴퓨터 프로그램에 대한 신뢰성 때문에 100% 인정받지 못하였음. 하지만 사용된 컴퓨터 프로그램의 문제가 발견된 것은 아님.
- 2005년에 G. Gonthier에 의해 두 사람의 증명이 옳았음이 검증됨.
$m$-색칠하기 문제 해결가능성 판단 알고리즘¶
- $m$ 이 1 또는 2인 경우: 쉽게 판단됨.
- $m = 3$ 인 경우: 효율적인 알고리즘 아직 찾지 못함.
- 즉, 임의의 평면 지도에 대해 서로 인접한 지역은 다른 색상을 갖도록 3 가지 색상만을 이용하여 색칠할 수 있는지 여부를 판단하는 일이 매우 어려움.
연습문제¶
문제 1¶
5-퀸 문제를 해결하는 되추적 알고리즘을 단계별로 설명하라.
앞서 소개한 n-퀸 알고리즘은 DFS 기법을 사용하며, 하나의 해답을 찾으면 바로 종료함. 따라서 아래 단계를 거치며 해답 하나를 구함.
- 첫째 퀸: 1행 1열에 위치시킴
- 둘째 퀸: 2행 3~5열이 유망함. 따라서 3열에 위치시킴.
- 셋째 퀸: 3행 5열만이 유일하게 유망함. 따라서 5열에 위치시킴.
- 넷째 퀸: 4행 2열만이 유일하게 유망함. 따라서 2열에 위치시킴.
- 다섯째 퀸: 5행 4열만이 유일하게 유망함. 따라서 4열에 위치시킴.

- 앞서 작성한
backtracking_search_queens()함수를 이용하여 확인하면 다음과 같음.
# 변수: 네 개의 퀸의 번호, 즉, 1, 2, 3, 4, 5
variables = [1, 2, 3, 4, 5]
# 도메인: 각각의 퀸이 자리잡을 수 있는 가능한 모든 열의 위치.
domains: Dict[int, List[int]] = {}
columns = [1, 2, 3, 4, 5]
for var in variables:
domains[var] = columns
backtracking_search_queens()
{1: 1, 2: 3, 3: 5, 4: 2, 5: 4}
문제 2¶
빨강(R), 초록(G), 파랑(B)이 주어졌을 때 되추적 알고리즘을 이용하여 아래 그래프를 색칠하는 과정을 단계별로 설명하라.
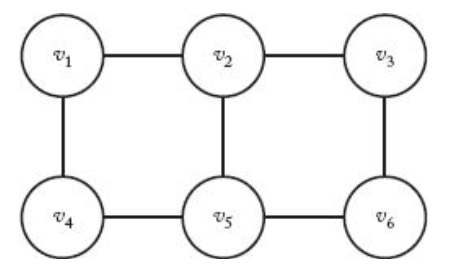
앞서 소개한 m-색칠하기 알고리즘은 DFS 기법을 사용하며, 하나의 해답을 찾으면 바로 종료함. 따라서 아래 단계를 거치며 해답 하나를 구함.
- v1: R, G, B가 유망하지만 먼저 R 선택
- v2: G, B가 유망하지만 먼저 G 선택
- v3: R, B가 유망하지만 먼저 R 선택
- v4: G, B가 유망하지만 먼저 G 선택
- v5: R, B가 유망하지만 먼저 R 선택
- v6: G, B가 유망하지만 먼저 G 선택
- 앞서 작성한
backtracking_search_colors()함수를 이용하여 확인하면 다음과 같음.
# 변수: 여섯 개 마디의 번호, 즉, 1, 2, 3, 4, 5, 6
variables = [1, 2, 3, 4, 5, 6]
# 도메인: 각각의 마디에 칠할 수 있는 색상 세 개(R, G, B)
domains: Dict[int, List[int]] = {}
columns = [1, 2, 3]
for var in variables:
domains[var] = columns
- 위 그래프에 의한 제약조건을 사용한 유망성 확인 함수는 다음과 같음.
def promissing_colors(variable: int, assignment: Dict[int, int]):
"""새로운 변수 variable에 값을 할당 하면서 해당 변수와 연관된 변수들 사이의 제약조건이
assignment에 대해 만족되는지 여부 확인
m-색칠하기 문제의 경우: 이웃마디의 상태에 따라 제약조건이 달라짐.
즉, 마디 variable에 할당된 색이 이웃마디의 색과 달라야 함.
이를 위해 각각의 마디가 갖는 이웃마디들의 리스트를 먼저 확인해야 함."""
# 각 마디에 대한 이웃마디의 리스트
constraints = {
1 : [2, 4],
2 : [1, 3, 5],
3 : [2, 6],
4 : [1, 5],
5 : [2, 4, 6],
6 : [3, 5]
}
for var in constraints[variable]:
if (var in assignment) and (assignment[var] == assignment[variable]):
return False
return True
- 실제로 빨강과 초록이 번갈아 사용됨을 아래와 같이 확인됨.
backtracking_search_colors()
{1: 1, 2: 2, 3: 1, 4: 2, 5: 1, 6: 2}