2절 단일출발점 최단경로: 다익스트라 알고리즘

• 문제: 가중치 포함 방향그래프의 한 특정 마디에서 임의의 다른 마디로 가는 최단경로 구하기

• 주의사항: 임의의 출발점이 아닌 하나의 고정된 하나의 마디에서 출발하는 경로만 대상으로 함.

• 최소비용 신장트리 문제와 비슷한 알고리즘으로 해결 가능

예제

• $v_1$에서 임의의 다른 마디로 가는 최단 경로 구하기

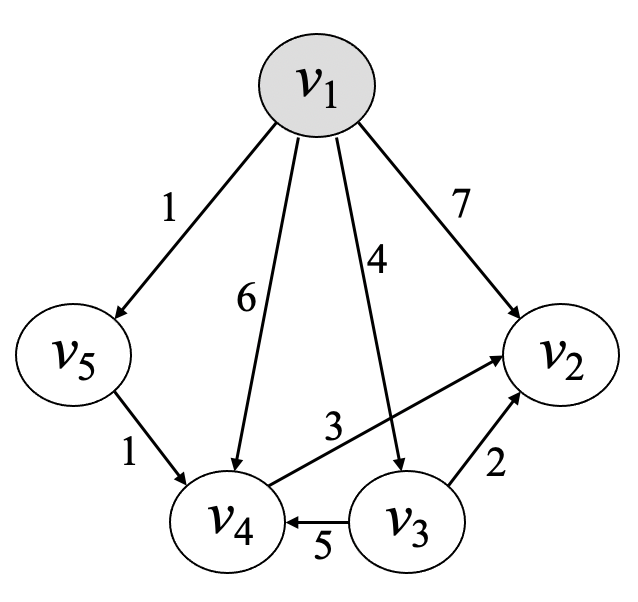
• 해답

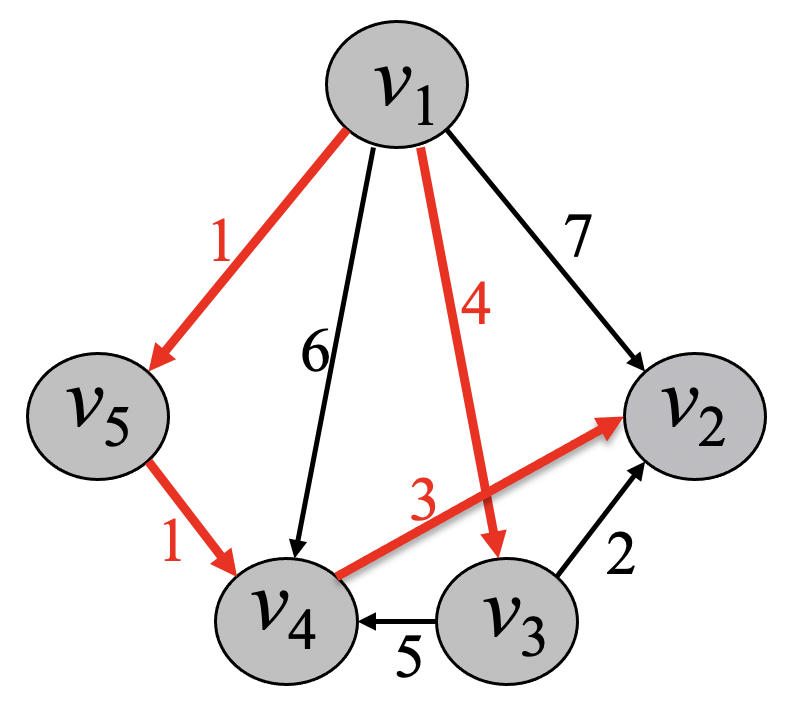
탐욕 알고리즘 적용

전제조건

• 가중치를 포함하고 연결된 방향그래프 $G$가 아래와 같이 주어졌음:

$$ G = (V, E) $$

• $V$: 마디들의 집합

• $E$: 이음선들의 집합(방향 있음)

다익스크라(Dijkstra) 알고리즘 기본 아디이어

$G = (V, E)$

$Y = \{ v_1 \}$
$F = \emptyset$

while (사례 미해결):

       - $v_1$에서 출발하여 $Y$에 속한 마디만 중간경로로 사용해서 갈 수 있는 마디 중에서
          $v_1$으로부터 가장 짧은 경로를 갖는 마디 $v \in (V-Y)$ 선택.

       - 선택된 마디를 $Y$에 추가.
       - 해당 마디 선택에 사용된 이음선을 $F$에 추가.

       if ($Y == V$):
              사례해결

예제

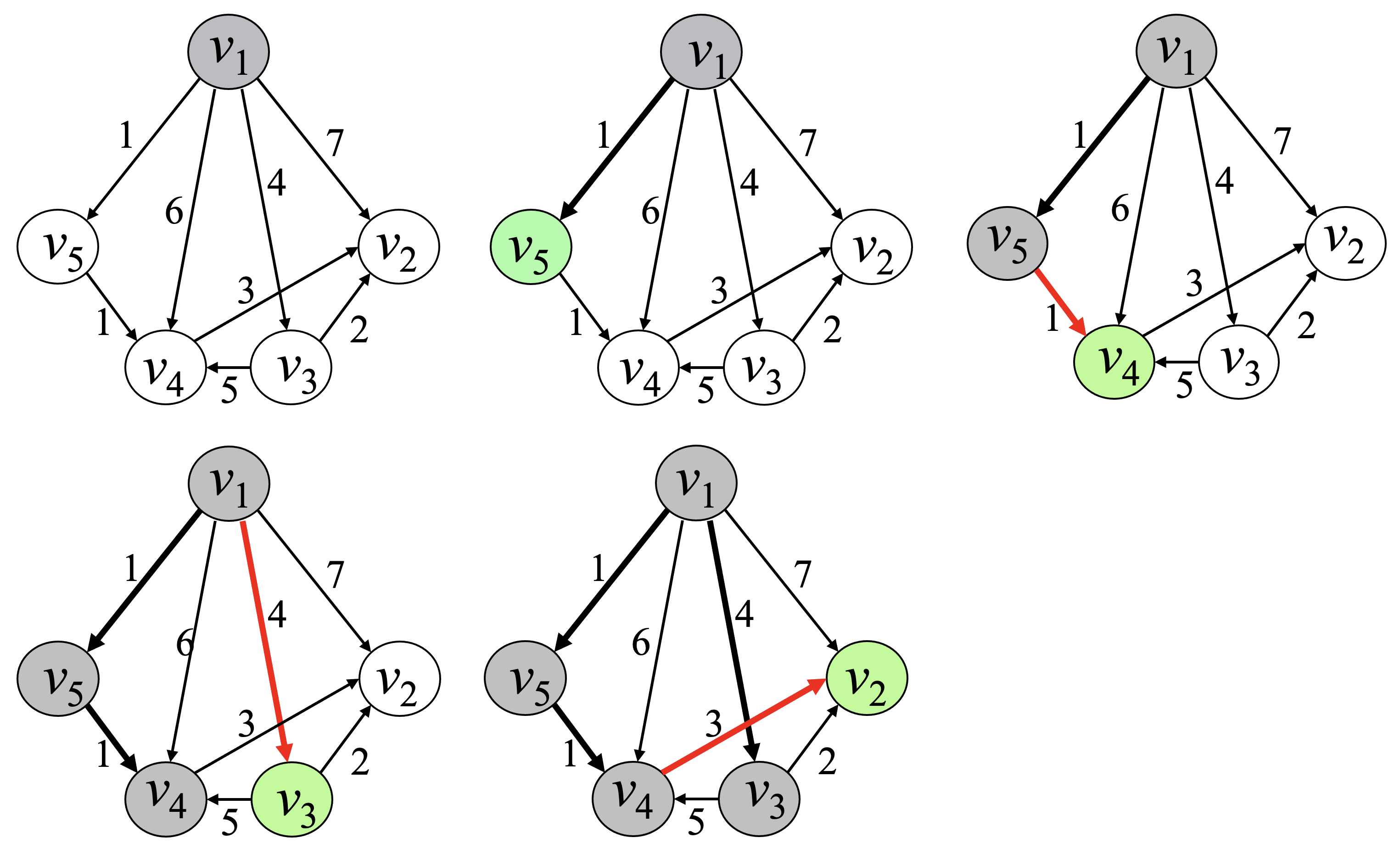
다익스트라 알고리즘의 최적여부 증명

• 프림 알고리즘에 대한 증명과 유사 (연습문제)
  • 두 집합 $Y$와 $F$가 변경될 때마나 $v_1$으로부터 각 마디까지의 최단거리가 변경되지 않음을 재귀적으로 증명해야 함.

다익스트라 알고리즘 구현

from math import inf
from collections import defaultdict

def dijkstra(W):
    V = len(W)
    F = defaultdict(list) # 최단경로를 구성하는 이음선들의 집합
    
    touch = [0] * V
    length = [W[0][i] for i in range(V)]
    length[0] = -1

    for _ in range(V-1):
        min = inf
        for i in range(V):
            if (0 < length[i] < min):
                min = length[i]
                vnear = i

        F[touch[vnear]].append(vnear)

        for i in range(V):
            if (length[vnear] + W[vnear][i] < length[i]):
                length[i] = length[vnear] + W[vnear][i]
                touch[i] = vnear
        
        length[vnear] = -1

    return F

W = [[0,     7,   4,   6,   1],
     [inf,   0, inf, inf, inf],
     [inf,   2,   0,   5, inf],
     [inf,   3, inf,   0, inf],
     [inf, inf, inf,   1,   0]]

dijkstra(W)

defaultdict(list, {0: [4, 2], 4: [3], 3: [1]})

코드 설명

• 신장트리 구현 코드와 거의 동일

• 차이점: length[vnear] = -1 명령문을 전체 반복문 맨 뒤로 옮겨야 함.
  • 신장트리 코드에서는 위치가 전혀 중요하지 않았음.

다익스트라 알고리즘 일정 시간복잡도 분석

• 입력크기: 마디 수 $n$

• 단위연산: 중첩 for 반복문

• 일정 시간복잡도: $n-1$ 번 반복되는 명령문 두 개가 $n-1$번 반복되는 반복문 안에 들어 있음. 따라서 다음이 성립:

$$ T(n) = 2(n-1)(n-1) = \Theta(n^2) $$

다익스트라 알고리즘 일반화

• 출발점을 $v_1$으로 고정하는 대신에 임의의 마디로 지정하기

• dijstra() 함수에 출발점을 추가하면 됨.

def dijkstra_gen(k, W):
    V = len(W)
    assert (0<= k < V)
    F = defaultdict(list) # 최단경로를 구성하는 이음선들의 집합
    
    touch = [k] * V
    length = [W[k][i] for i in range(V)]
    length[k] = -1 # v_k를 출발 마디로 지정

    for _ in range(V-1):
        min = inf
        for i in range(V):
            if (0 < length[i] < min):
                min = length[i]
                vnear = i
                
        if min == inf:
            return "일부 경로가 없어요."

        F[touch[vnear]].append(vnear)

        for i in range(V):
            if (length[vnear] + W[vnear][i] < length[i]):
                length[i] = length[vnear] + W[vnear][i]
                touch[i] = vnear
        
        length[vnear] = -1

    return F

dijkstra_gen(0, W)

defaultdict(list, {0: [4, 2], 4: [3], 3: [1]})

dijkstra_gen(2, W)

'일부 경로가 없어요.'

dijkstra_gen(4, W)

'일부 경로가 없어요.'

5절 탐욕 알고리즘과 동적계획법 알고리즘 비교: 0-1 배낭채우기 문제

• 최단경로를 계산하는 문제를 두 가지 방식으로 풀었음. 하지만 방식에 따라 복잡도가 다름.
  • 동적계획법(3장 2절): $\Theta(n^3)$
  • 탐욕 알고리즘(2절): $\Theta(n^2)$

• 일반적으로 탐욕 알고리즘이 더 간단하고 더 효율적임.

• 하지만 탐욕 알고리즘이 항상 최적의 해를 제공하는 것은 아니며, 그런 경우에도 증명이 매우 어려울 수 있음.

0-1 배낭채우기 문제

• $n$개의 주어진 물건들 중에서, 한정된 용량($W$)의 배낭에 물건을 골라 넣었을때 얻을 수 있는 최대 값어치를 찾는 조합 최적화 문제

무차별 대입 방식(brute force approach)

• 배낭에 넣을 수 있는 모든 물건의 조합 살피기

• $n$개의 물건이 있을 때 총 $2^n$개의 조합 존재

• 따라서 $\Theta(2^n)$의 시간복잡도를 가짐. 따라서 실용성 없음.

탐욕 알고리즘 예제

물건1: 50만원, 5kg
물건2: 60만원, 10kg
물건3: 140만원, 20kg

• W = 30일 경우 최적의 해

    140 + 60 = 200(만원)

• 탐욕 알고리즘은 선택 전략과 경우에 따라 최적의 해 제공여부가 달라짐.

전략 1

• 가장 값비싼 물건 선택하기

• 위 예제에서는 최적의 해를 제공하지만, 경우에 따라 달라짐.

  • 반례: 물건4가 아래와 같이 추가되는 경우 가장 값비싼 문건을 먼저 선택하는 전략은 최적의 해를 제공하지 않음. (이유는?)

      물건1: 50만원, 5kg
      물건2: 60만원, 10kg
      물건3: 140만원, 20kg
      물건4: 30만원, 2kg

전략 2

• 무게당 값어치가 가장 큰 물건 선택

    물건1 1kg당 값어치: 10만원
    물건2 1kg당 값어치: 6만원
    물건3 1kg당 값어치: 7만원

  따라서 아래 물건 선택

    50만원: 5kg
    140만원: 20kg
    ------------
    190만원: 25kg

  최적의 해 아님.

• 하지만 물건4가 추가되면 최적의 해를 제공함.

    물건1 1kg당 값어치: 10만원
    물건2 1kg당 값어치: 6만원
    물건3 1kg당 값어치: 7만원
    물건4 1kg당 값어치: 15만원

  따라서 아래 물건 선택

    30만원: 2kg
    50만원: 5kg
    140만원: 20kg
    ------------
    220만원: 27kg

  최적의 해 아님.

결론

• 탐욕 알고리즘은 0-1 배낭채우기 문제를 일반적으로 해결할 수 없음.

동적계획법 알고리즘

• 참조: 고전 컴퓨터 알고리즘 인 파이썬, 9장

• 이항계수 동적계획법 알고리즘과 유사.

• 아래 조건을 만족하는 (n+1,W+1) 모양의 2차원 행렬 $P$ 생성

\begin{align*} P[i][w] &= \text{총 무게가 $w$를 넘기지 않는 조건하에서} \\ & \quad\,\text{처음 $i$ 개의 물건만을 이용해서 얻을 수 있는 최대 이익} \end{align*}

주어진 조건

• $i$ 번째 물건의 무게와 값어치 ($0 \le i \le n$)
  • 무게: $w_i$
  • 값어치: $p_i$

$P[i][j]$의 재귀식

• 초기값: $i = 0$인 경우
  • 물건을 전혀 사용하지 못하기 때문에 물건을 전혀 배낭에 담지 못함.
  • 따라서 모든 $0 \le w \le W$에 대해 다음 성립:

$$ P[0][w] = 0 $$

• 귀납단계: $i>0$ 이라고 가정.
  • 3 가지 경우 존재

• 경우 1
  • $w_i > w$
  • 즉, $i$번째 물건을 가방에 전혀 넣을 수 없음.
  • 따라서 아래 재귀식 성립

$$ P[i][w] = P[i-1][w] $$

• 경우 2
  • $w_i \le w$ 이지만 $i$번째 물건이 최적 조합에 사용되지 않는 경우

$$ P[i][w] = P[i-1][w] $$

• 경우 3
  • $w_i \le w$ 이고 $i$번째 물건이 최적 조합에 사용되는 경우

$$ P[i][w] = p_i + P[i-1][w-w_i] $$

• 정리하면:

$$ P[i][w] = \begin{cases} \max(P[i-1][w], p_i + P[i-1][w-w_i]) & \text{if } w_i \le w, \\ & \\ P[i-1][w] & \text{if } w_i > w \end{cases} $$

• 최적화 원칙도 성립함.

동적계획법 알고리즘 구현

• 물건들의 클래스 지정
  • NamedTuple 클래스를 활용하면 쉽게 자료형 클래스를 지정할 수 있음.

from typing import NamedTuple

class Item(NamedTuple):
    name: str
    weight: int
    value: float

예제

<그림 출처:배낭 문제: 위키피디아>

items = [Item("item1", 1, 1),
         Item("item2", 1, 2),
         Item("item3", 2, 2),
         Item("item4", 4, 10),
         Item("item5", 12, 4)]

• 각 물건 조합의 최상의 결과를 알려주는 표 작성 알고리즘

# 아이템(물건) 개수와 용량 한도
n = len(items)
W = 15

• 행렬 P를 영행렬로 초기화 하기

# (n+1,W+1) 모양

P = [[0.0 for _ in range(W+1)] for _ in range(n+1)]

• $P$ 행렬의 항목을 1번행부터 행단위로 업데이트함.
  • 0번행과 0번열은 그대로 0으로 둠.

for i, item in enumerate(items):         # 행 인덱스(물건 번호)는 0부터 시작함에 주의
    
    wi = item.weight                     # (i+1) 번째 아이템 무게
    pi = item.value                      # (i+1) 번째 아이템 가치

    for w in range(1, W + 1):            # 열 인덱스(용량 한도) 역시 0부터 시작
        
        previous_items_value = P[i][w]   # i번 행값을 이미 계산하였음. 예를 들어, P[0][w] = 0.

        if w >= wi:                      # 현재 아이템의 가방에 들어갈 수 있는 경우

            previous_items_value_without_wi = P[i][w - wi]

            P[i+1][w] = max(previous_items_value,
                            previous_items_value_without_wi + pi)

        else:                            # 현재 아이템이 너무 무거운 경우
            P[i+1][w] = previous_items_value

• 위 과정을 하나의 함수로 지정

def knapsack(items, W):
    """
    items: 아이템(물건)들의 리스트
    W: 최대 저장용량
    """
    
    # 아이템(물건) 개수
    n = len(items)

    # P[i][w]를 담는 2차원 행렬을 영행렬로 초기화
    # (n+1) x (W+1) 모양
    P = [[0.0 for _ in range(W+1)] for _ in range(n+1)]

    for i, item in enumerate(items):
        wi = item.weight                     # (i+1) 번째 아이템 무게
        pi = item.value                      # (i+1) 번째 아이템 가치

        for w in range(1, W + 1):
            previous_items_value = P[i][w]   # i번 행값을 이미 계산하였음. i는 0부터 시작함의 주의할 것
            if w >= wi:                      # 현재 아이템의 무게가 가방에 들어갈 수 있는 경우
                previous_items_value_without_wi = P[i][w - wi]
                P[i+1][w] = max(previous_items_value,
                                  previous_items_value_without_wi + pi)
            else:
                P[i+1][w] = previous_items_value
                
    return P

• 최적의 조합을 알려주는 알려주는 함수
  • 생성된 2차 행렬 $P$로부터 최적의 조합 찾아낼 수 있음.

def solution(items, W):
    P = knapsack(items, W)
    n = len(items)
    w = W
        
    # 선택 아이템 저장
    selected = []

    # 선택된 아이템을 역순으로 확인
    for i in range(n, 0, -1): 
        if P[i - 1][w] != P[i][w]:          # (i-1) 번째 아이템이 사용된 경우. 인덱스가 0부터 출발함에 주의
            selected.append(items[i - 1])
            w -= items[i - 1].weight        # (i-1) 번째 아이템의 무게 제거 
    return selected

• 획득된 최대 값어치를 알려주는 함수

def max_value(items, W):
    selected = solution(items, W)
    sum = 0
    
    for item in selected:
        sum += item.value
    
    return sum    

활용 1

for item in solution(items, 15):
    print(item)

Item(name='item4', weight=4, value=10)
Item(name='item3', weight=2, value=2)
Item(name='item2', weight=1, value=2)
Item(name='item1', weight=1, value=1)

max_value(items, 15)

15

활용 2

• 행렬 P를 살펴보기 위한 좀 작은 용량의 배낭채우기 문제

items2 = [Item("item1", 1, 5),
         Item("item2", 2, 10),
         Item("item3", 1, 15)]

• 최대용향 3까지 허용할 때 최대 값어치로 이루어진 (4, 4) 모양의 행렬 $P$

knapsack(items2, 3)

[[0.0, 0.0, 0.0, 0.0],
 [0.0, 5.0, 5.0, 5.0],
 [0.0, 5.0, 10.0, 15.0],
 [0.0, 15.0, 20.0, 25.0]]

• 행렬 $P$로부 최적의 조합 알아내기
  • 오직 아래 등식이 성립할 때 $i$ 번째 아이템이 선택됨.

$$ P[i][w] \neq P[i-1][w], \qquad P[i][w] = p_i + P[i-1][w - w_i] $$

• 따라서 $P[4][4]$에서 시작하여 역순으로 사용되는 아이템 확인 가능

for item in solution(items2, 3):
    print(item)

Item(name='item3', weight=1, value=15)
Item(name='item2', weight=2, value=10)

NamedTuple 클래스를 사용하지 않는 경우

• 기본 클래스 정의를 활용하면 해야할 일이 좀 더 많아짐.

class Item1:
    def __init__(self, name, weight, value):
        self.name = name
        self.weight = weight
        self.value = value

items3 = [Item1("item1", 1, 1),
         Item1("item2", 1, 2),
         Item1("item3", 2, 2),
         Item1("item4", 4, 10),
         Item1("item5", 12, 4)]

for item in solution(items3, 15):
    print(item)

<__main__.Item1 object at 0x7fc96e03a8b0>
<__main__.Item1 object at 0x7fc96e03abb0>
<__main__.Item1 object at 0x7fc96e03a820>
<__main__.Item1 object at 0x7fc96e03a9a0>

• __str__() 메서드 구현 필요

class Item1:
    def __init__(self, name, weight, value):
        self.name = name
        self.weight = weight
        self.value = value
        
    def __str__(self):
        return 'Item(' + self.name + ', ' + str(self.weight) + ', ' + str(self.value) + ')'

items4 = [Item1("item1", 1, 1),
         Item1("item2", 1, 2),
         Item1("item3", 2, 2),
         Item1("item4", 4, 10),
         Item1("item5", 12, 4)]

for item in solution(items4, 15):
    print(item)

Item(item4, 4, 10)
Item(item3, 2, 2)
Item(item2, 1, 2)
Item(item1, 1, 1)

시간복잡도

• 입력크기: 물건(item) 수 $n$과 가장 최대 용량 $W$
• 단위연산: 채워야 하는 행렬 $P$의 크기

$$ n\, W \in \Theta(n\, W) $$

절대 선형이 아님!

• 예를 들어, $W = n!$이면, $\Theta(n\cdot n!)$의 복잡도가 나옴.

• 즉, $W$값에 복잡도가 절대적으로 의존함.

개선된 알고리즘

• 행렬 $P$ 전체를 계산할 필요 없음.

• $P[n][W]$ 을 계산하기 위해 필요한 값들만 계산하도록 하면 됨.
  • 교재 참조

• 이렇게 구현하면 아래의 복잡도를 갖는 알고리즘 구현 가능

$$ O(\min(2^n, n\, W)) $$

연습문제

문제 1

dijkstra() 함수가 항상 최단경로에 대한 정보를 생성함을 증명하라.

문제 2

dijkstra() 함수는 최단경로에 포함된 이음선만 찾는다. 최단경로와 최단길이를 반환하는 함수 dijkstra_path() 함수를 구현하라.

문제 3

아래 표로 표현되는 방향그래프의 마디 v4에서 다른 마디로 가는 최단경로를 구하는 과정을 단계별로 설명하라.

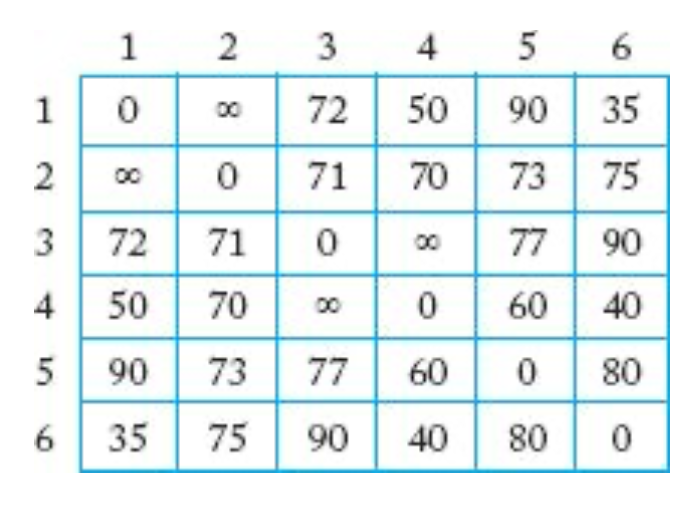
• 위 표를 2차원 행렬로 표현하면 다음과 같음.

W = [[  0, inf,  72,  50,  90,  35],
     [inf,   0,  71,  70,  73,  75],
     [ 72,  71,   0, inf,  77,  90],
     [ 50,  70, inf,   0,  60,  40],
     [ 90,  73,  77,  60,   0,  80],
     [ 35,  75,  90,  40,  80,   0]]

• 다익스트라 알고리즘에 의해 v5에서 각 마디로 가는 최단경로를 찾는 과정은 다음과 같음.

  • Y = {5}
    • v5에서 Y에 속한 마디들만을 통해 갈 수 있는 가장 가까운 마디는 거리가 60인 v4
  • Y = {5, 4}
    • v5에서 Y에 속한 마디들만을 통해 갈 수 있는 가장 가까운 마디는 v5에서 직접 연결되고 거리가 73인 v2
    • v4롤 통해 Y에 속하지 않는 마디로 가는 경로는 모두 73보다 크기 때문임.
      • length(v5 -> v4 -> v?) >= 60 + 40 = 100
  • Y = {5, 4, 2}
    • v5에서 Y에 속한 마디들만을 통해 갈 수 있는 가장 가까운 마디는 v5에서 직접 연결되고 거리가 77인 v3
    • v2롤 통해 Y에 속하지 않는 마디로 가는 경로는 모두 77보다 크기 때문임.
      • length(v5 -> v2 -> v?) >= 73 + 70 = 143

• 다익스트라 알고리즘(이어짐)

  • Y = {5, 4, 2, 3}
    • v5에서 Y에 속한 마디들만을 통해 갈 수 있는 가장 가까운 마디는 v5에서 직접 연결되고 거리가 80인 v6
    • v3롤 통해 Y에 속하지 않는 마디로 가는 경로는 모두 80보다 크기 때문임.
      • length(v5 -> v3 -> v?) >= 77 + 71 = 147
  • Y = {5, 4, 2, 3, 6}
    • v5에서 Y에 속한 마디들만을 통해 갈 수 있는 가장 가까운 마디는 v5에서 직접 연결되고 거리가 90인 v1
    • v6롤 통해 Y에 속하지 않는 마디로 가는 경로는 모두 90보다 크기 때문임.
      • length(v5 -> v6 -> v?) >= 80 + 35 = 115
  • Y = {5, 4, 2, 3, 6, 1}

• 실제로 dijkstra_gen() 함수를 이용한 아래 결과와 동일함.
• 인덱스에 1을 더해야 함에 주의할 것.

dijkstra_gen(4,W)

defaultdict(list, {4: [3, 1, 2, 5, 0]})