4장 탐욕 알고리즘¶
주요 내용¶
- 1절 최소비용 신장트리: 프림 알고리즘
- 2절 단일출발점 최단경로: 다익스트라 알고리즘
- 5절 탐욕 알고리즘과 동적계획법 알고리즘 비교: 0-1 배낭채우기 문제
탐욕 알고리즘이란?¶
- 선택 순간의 최적(locally optimal) 대상을 선택하는 기법
- 동적계획법과 마찬가지로 최적화 문제를 풀기 위해 주로 사용됨.
- 차이점: 입력사례를 분할하지 않음.
예제: 거스름돈 문제¶
- 문제: 거스름돈 360원 돌려주기
- 조건: 사용하는 동전 개수 최소화하기
- 동전 종류
- 500원
- 250원
- 100원
- 50원
- 10원
해결책: 탐욕 알고리즘 활용¶
- 가장 큰 액수의 동전부터 최대한 많이 사용
500원: 0개
250원: 1개
100원: 1개
50원: 0개
10원: 1개- 항상 동전의 개수가 최소가 되도록 거스름돈을 돌려줄 수 있음.
- 증명 생략
탐욕 알고리즘의 한계¶
- 탐욕 알고리즘이 항상 최적의 해답을 제시하지는 못함.
- 따라서 탐욕적 알고리즘을 적용하여 얻은 결과가 최적의 해답인지 여부를 따로 검증해야 함.
반례¶
- 160원을 거슬러주어야 하는데 동전 종류가 다음과 같은 경우
- 120원
- 100원
- 50원
- 10원
- 탐욕 알고리즘 해법: 5개 동전 필요
120원: 1개
100원: 0개
50원: 0개
10원: 4개- 최적 해법: 3개 동전 필요
120원: 0개
100원: 1개
50원: 1개
10원: 1개탐욕 알고리즘 기본 아이디어¶
- 공집합에서 출발하여 해당 집합에 원소를 아래 과정을 거쳐 문제의 해답을 얻을 때까지 추가
1) 선택과정: 지정된 기준에 따라 집합에 추가할 최적의 원소 선택.
2) 적절성 검사: 선택된 원소가 추가된 새로운 집합의 적절성 판단
3) 해답점검: 새로운 집합이 문제의 해답인지 여부 판단.
- 해답이면 종료.
- 그렇지 않으면 선택과정부터 다시 반복
1절 최소비용 신장트리¶
가중치 포함 비방향그래프¶
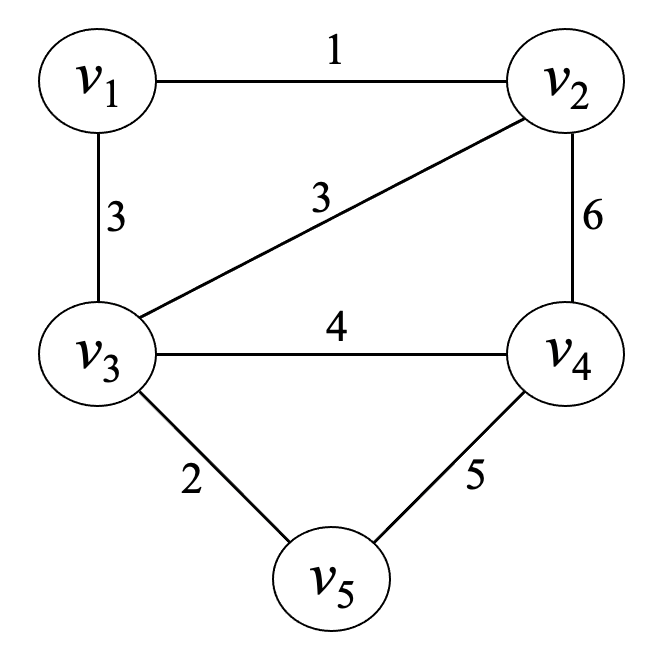
- 가중치: 음이 아닌 수.
- 이음선(edge, 변): 방향 없음.
- 두 마디 사이에 단순히 "이음선이 있다"라고만 말함.
경로¶
- 경로(path): 연결된 이음선으로 이루어진 마디의 나열
- 마디 $u$에서 마디 $v$로 가는 경로가 존재하면, $v$에서 $u$로 가는 경로도 존재. (이음선에 방향성이 없기 때문)
- 두 마디의 연결성 = 두 마디 사이에 경로의 존재 여부
- 연결된 그래프: 모든 마디 사이에 경로가 존재하는 그래프
단순순환경로(simple cycle)와 트리¶
- 어떤 마디에서 출발하여 다시 돌아오는 경로에 서로 다른 3개의 마디가 있고, 경로상의 모든 마디가 서로 다른 경로
- 비순환적 비방향그래프: 단순순환경로를 전혀 포함하지 않는 비방향그래프
- 트리: 연결된 비순환적 비방향그래프
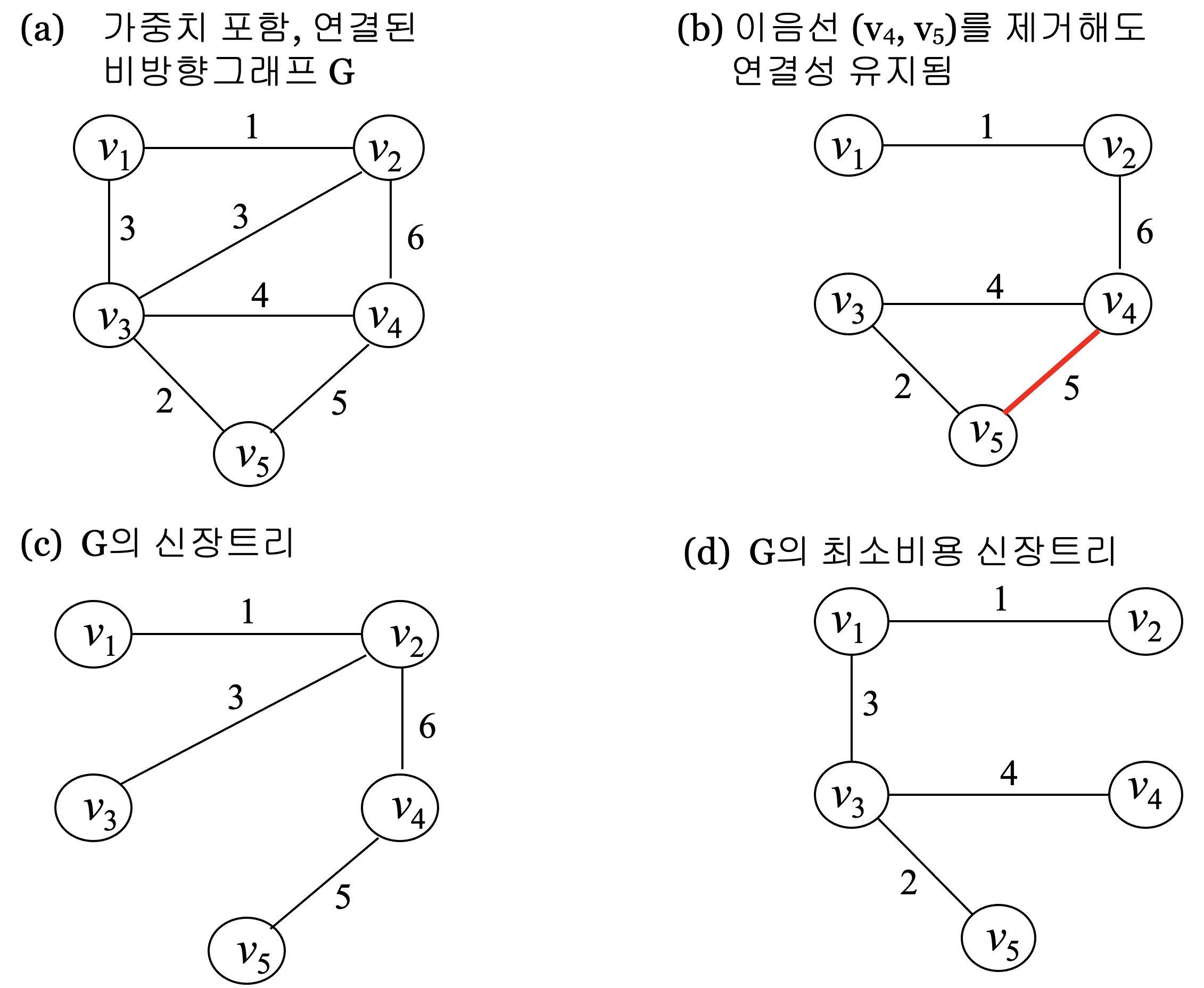
신장트리(spanning tree)¶
- 가정: 가중치를 포함하며 연결된 비방향그래프 G가 주어졌음.
- G의 신장트리: G의 마디는 그대로 두면서 이음선의 일부를 제거하여 만들어진 트리
- G의 최소비용 신장트리: 트리에 포함된 이음선의 가중치들의 합이 최소인 G의 신장트리
신장트리의 특징¶
- 모든 신장트리가 최소비용 신장트리는 아님.
- 여러 개의 최소비용 신장트리 존재 가능.
예제¶
최소비용 신장트리 활용 예제¶
- 도로건설: 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
- 통신: 통신선의 길이가 최소가 되도록 통신케이블 망을 구성하는 문제
- 배관: 배관의 총 길이가 최도가 되도록 연결하는 문제
최소비용 신장트리 구하기: 무작정 방법(brute-force method)¶
- 알고리즘: 모든 신장트리를 확인하여 최소비용 신장트리 선택하기
- 복잡도: 최악의 경우 지수함수 복잡도보다 나쁨. 예를 들어, 아래 복잡도보다 나쁨.
$$
\Theta(n^{n-2})
$$
프림(Prim) 알고리즘¶
전제조건¶
- 가중치를 포함하고 연결된 비방향그래프 $G$가 아래와 같이 주어졌음:
$$
G = (V, E)
$$
- $V$: 마디들의 집합
- $E$: 이음선들의 집합
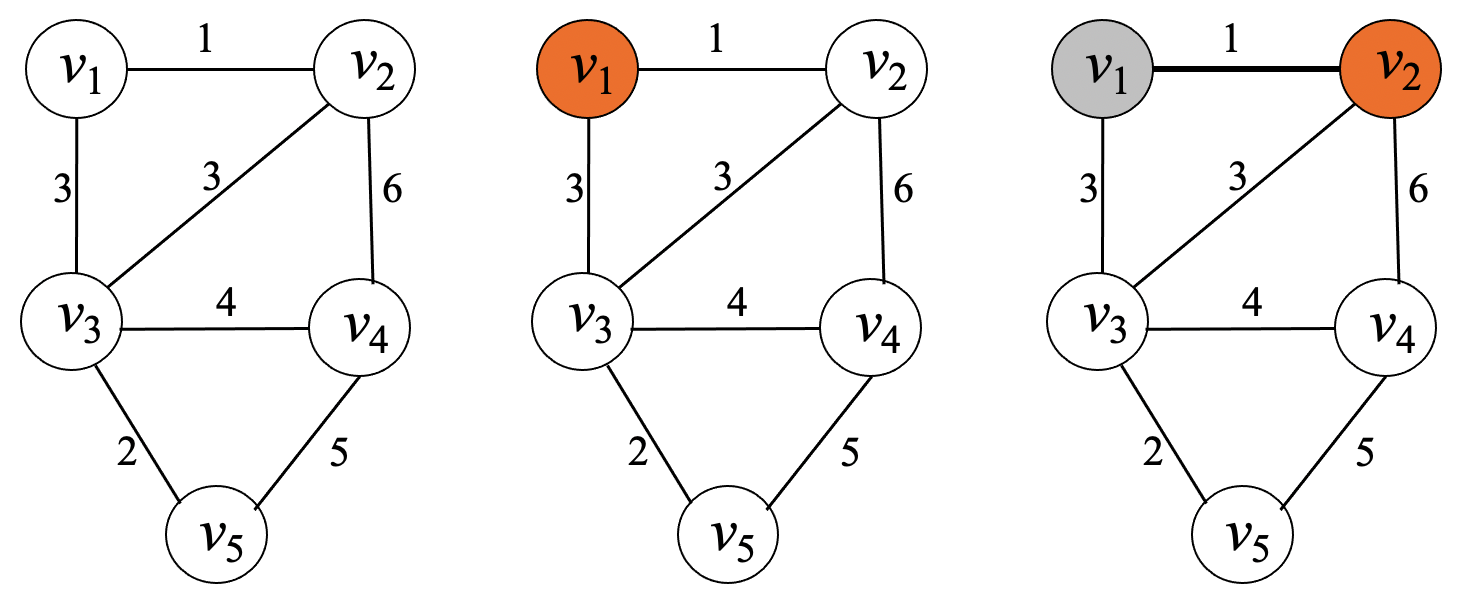
프림 알고리즘 기본 아디이어¶
$G = (V, E)$
$Y = \{ v_1 \}$
$F = \emptyset$
while (사례 미해결):
$(V-Y)$에 속한 마디 중에서 $Y$와 가장 가까운(최소거리) 마디 선택
해당 마디를 $Y$에 추가
해당 마디 선택에 사용된 이음선을 $F$에 추가
if ($Y == V$):
사례해결
예제¶
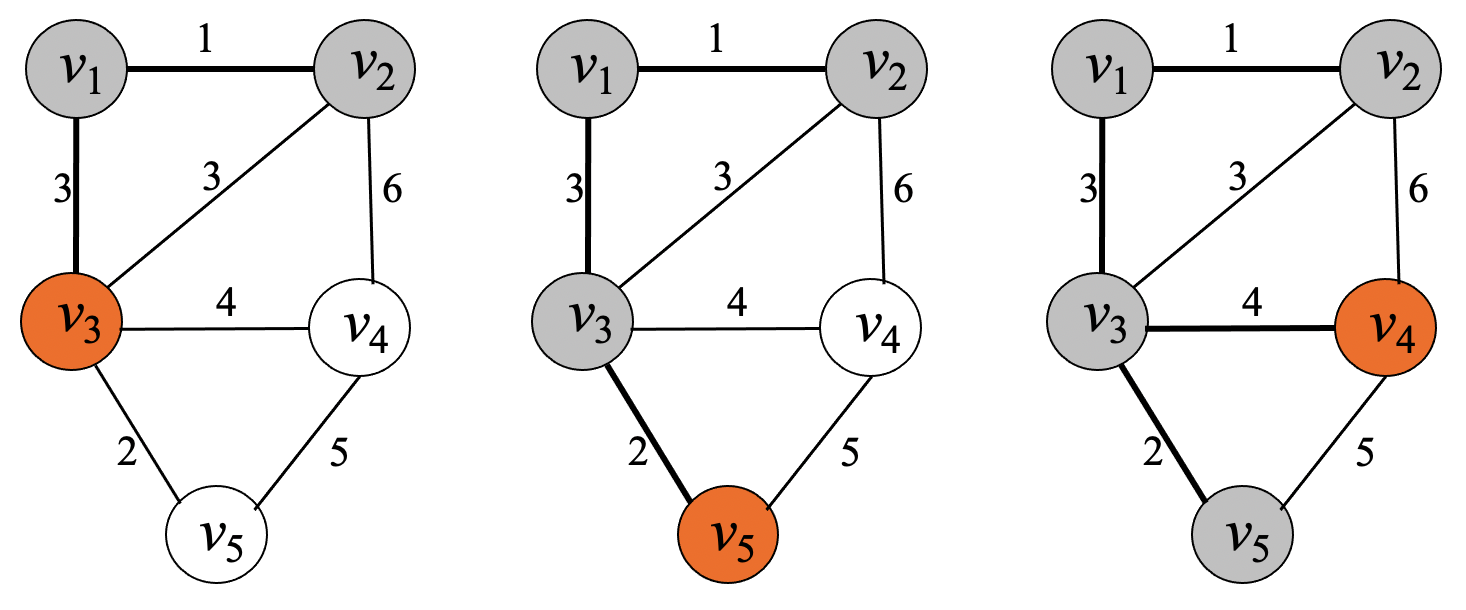
프림 알고리즘의 최적여부 증명¶
- 프림 알고리즘이 항상 최소비용 신장트리를 생성하는지 증명해야 함.
- 결과가 신장트리라는 것은 확실함.
- $(V == Y)$ 일 때 종료.
- 모든 마디가 서로 연결됨.
- 단순순환경로 존재하지 않음.
- 하지만 최소비용 신장트리 여부는 불확실함.
유망한 이음선 집합¶
전제:
$$G = (V, E) \quad\text{이고}\quad F \subseteq E$$
- $F$에 이음선을 추가하여 최소비용 신장트리를 만들 수 있을 때 "$F$는 유망하다(promissing)" 라고 부름.
보조정리¶
- 전제 1: $G = (V, E)$ 이고 $F (\subseteq E)$는 유망함.
- 전제 2: $Y$는 $F$에 사용된 마디들의 집합
- 전제 3: $Y$에 있는 정점과 $(V-Y)$에 있는 정점을 잇는 이음선 중에서 가중치가 가장 적은 이음선 중에 하나가 $e$.
- 결론: $F \cup \{ e \}$ 또한 유망함.
보조정리 증명 (그림으로 설명)¶
정리¶
- 프림 알고리즘은 항상 최소비용 신장트리를 생성한다.
증명 (귀납법 사용)¶
- 귀납법을 사용하여 while 반복문에서 확장되는 $F$가 항상 유망하다는 것을 증명함.
- 귀납기초: 공집합은 당연히 유망함.
- 귀납단계: 보조정리에 의해 while 반복문에서 확장되는 $F$는 언제나 유망함.
- 귀납가정: while 반복문이 시작할 때 $F$가 유망하다고 가정
- 귀납절차: 보조정리에 의해 $F\cup\{ e \}$도 유망함. (알고리즘 참조)
- 귀납증명 완료
프림 알고리즘 구현¶
In [1]:
from math import inf
from collections import defaultdict
In [2]:
def prim(W):
V = len(W) # 마디: 그래프 행의 인덱스를 마디 이름으로 사용
F = defaultdict(list) # 신장트리에 포함될 이음선들의 집합.
# 키: 마디,
# 키값: 추가되는 이음선에 사용된 다른 마디들의 리스트
nearest = [0] * V # i번 인덱스 값: 신장트리에 속한 마디 중 가장 가까운 마디
distance = [W[0][i] for i in range(V)] # i번 인덱스 값: nearest[i]와 i를 잇는
# 이음선의 가중치. -1이면 이미 신장트리에 포함된 것으로 간주
distance[0] = -1 # V0 는 이미 포함되어 있다고 가정
for _ in range(V-1): # 신장트리에 속할 이음선을 모든 마디가 선택될 때가지 하나씩 추가
# distance 정보를 이용하여 아직 신장트리에 속하지 않으면서 가장 가까운 마디 선택
min = inf
for i in range(1, V):
if (0 < distance[i] < min):
min = distance[i]
vnear = i
# 선택된 마디와 가장 가까운 마디 사이의 이음선을 신장트리에 추가
F[nearest[vnear]].append(vnear)
distance[vnear] = -1 # 선택된 마디 표시
# 모든 마디를 대상으로 distance와 nearest 업데이트 (F가 수정되었기 때문)
for i in range(1, V):
if W[i][vnear] < distance[i]:
distance[i] = W[i][vnear]
nearest[i] = vnear
return F # 신장트리 반환
In [3]:
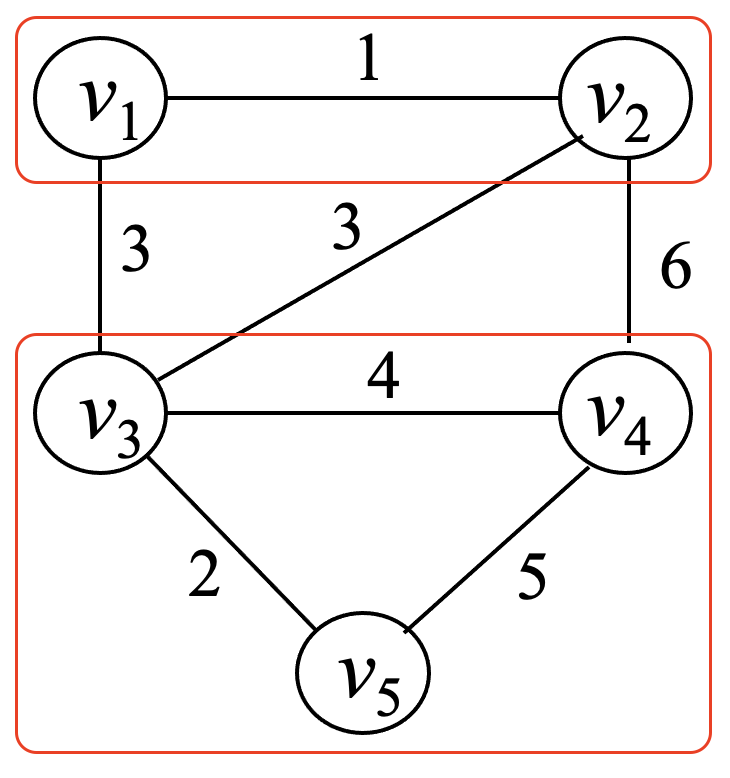
W = [[0, 1, 3, inf, inf],
[1, 0, 3, 6, inf],
[3, 3, 0, 4, 2 ],
[inf, 6, 4, 0, 5 ],
[inf, inf, 2, 5, 0 ]]
In [4]:
prim(W)
Out[4]:
defaultdict(list, {0: [1, 2], 2: [4, 3]})
코드 설명¶
V = len(W) # 마디: 그래프 행의 인덱스를 마디 이름으로 사용
F = defaultdict(list) # 신장트리에 포함될 이음선들의 집합.
# 키: 마디,
# 키값: 추가되는 이음선에 사용된 다른 마디들의 리스트
nearest = [0] * V # i번 인덱스 값: 신장트리에 속한 마디 중 가장 가까운 마디
distance = [W[0][i] for i in range(V)] # i번 인덱스 값: nearest[i]와 i를 잇는 이음선의 가중치
# -1 이면 이미 신장트리에 포함된 것으로 간주
distance[0] = -1 # V0 는 이미 포함되어 있다고 가정
for _ in range(V-1): # 신장트리에 속할 이음선을 모든 마디가 선택될 때가지 하나씩 추가
# distance 정보를 이용하여 아직 신장트리에 속하지 않으면서 가장 가까운 마디 선택
min = inf
for i in range(1, V):
if (0 < distance[i] < min):
min = distance[i]
vnear = i
# 선택된 마디와 가장 가까운 마디 사이의 이음선을 신장트리에 추가
F[nearest[vnear]].append(vnear)
distance[vnear] = -1 # 선택된 마디 표시
# 모든 마디를 대상으로 distance와 nearest 업데이트 (F가 수정되었기 때문)
for i in range(1, V):
if W[i][vnear] < distance[i]:
distance[i] = W[i][vnear]
nearest[i] = vnear
프림 알고리즘 일정 시간복잡도 분석¶
- 입력크기: 마디 수 $n$
- 단위연산: 중첩 for 반복문
- 일정 시간복잡도: $n-1$ 번 반복되는 명령문 두 개가 $n-1$번 반복되는 반복문 안에 들어 있음. 따라서 다음이 성립:
$$
T(n) = 2(n-1)(n-1) = \Theta(n^2)
$$
연습문제¶
문제 1¶
아래 비방향그래프의 최소신장트리를 찾는 과정을 단계별로 묘사하라.
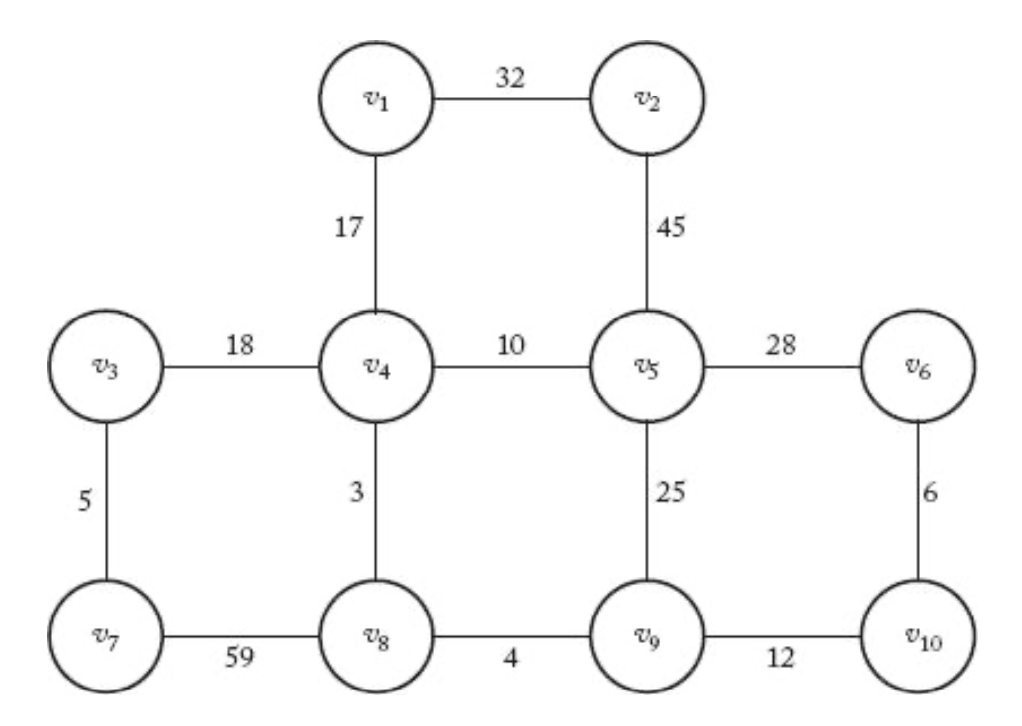
신장트리에 추가되는 이음선의 순서는 다음과 같음:
- Y = {1}
- v4-v1의 거리가 17로 가장 짧음.
- Y = {1, 4}
- v8-v4의 거리가 3으로 가장 짧음.
- Y = {1, 4, 8}
- v9-v8의 거리가 4로 가장 짧음.
- Y = {1, 4, 8, 9}
- v5-v4의 거리가 10으로 가장 짧음.
- Y = {1, 4, 8, 9, 5}
- v10-v9의 거리가 12로 가장 짧음.
- Y = {1, 4, 8, 9, 5, 10}
- v6-v10의 거리가 6으로 가장 짧음.
- Y = {1, 4, 8, 9, 5, 10, 6}
- v3-v4의 거리가 18로 가장 짧음.
- Y = {1, 4, 8, 9, 5, 10, 6, 3}
- v7-v3의 거리가 5로 가장 짧음.
- Y = {1, 4, 8, 9, 5, 10, 6, 3, 7}
- v2-v1의 거리가 32로 가장 짧음.
- Y = {1, 4, 8, 9, 5, 10, 6, 3, 7, 2}
- Y = {1}
- 아래 그래프에서 확인할 수 있음. 빨강색 숫자는 최소비용신장트리에 추가되는 순서를 가리킴.
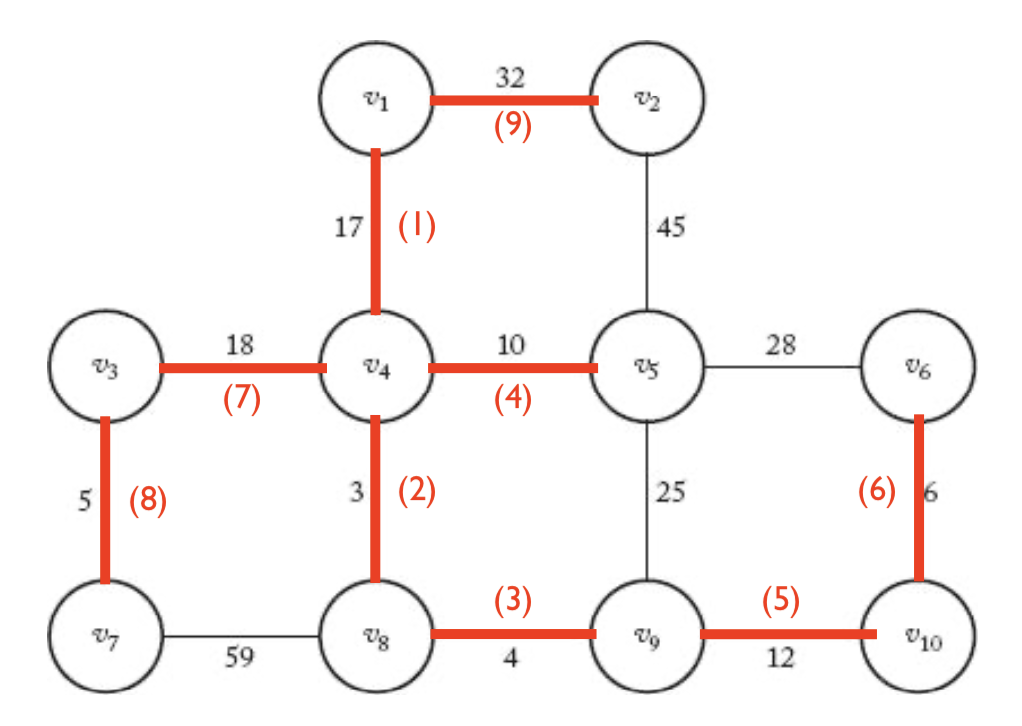
확인하기¶
- 위 비방향그래프를 2차원 행렬로 표기하면 다음과 같음.
In [5]:
W = [[ 0, 32, inf, 17, inf, inf, inf, inf, inf, inf],
[ 32, 0, inf, inf, 45, inf, inf, inf, inf, inf],
[inf, inf, 0, 18, inf, inf, 5, inf, inf, inf],
[ 17, inf, 18, 0, 10, inf, inf, 3, inf, inf],
[inf, 45, inf, 10, 0, 28, inf, inf, 25, inf],
[inf, inf, inf, inf, 28, 0, inf, inf, inf, 6],
[inf, inf, 5, inf, inf, inf, 0, 59, inf, inf],
[inf, inf, inf, 3, inf, inf, 59, 0, 4, inf],
[inf, inf, inf, inf, 25, inf, inf, 4, 0, 12],
[inf, inf, inf, inf, inf, 6, inf, inf, 12, 0]]
- 따라서 아래와 같이 최소비용신장트리를 확인됨.
In [6]:
prim(W)
Out[6]:
defaultdict(list, {0: [3, 1], 3: [7, 4, 2], 7: [8], 8: [9], 9: [5], 2: [6]})