6절 외판원 문제¶
외판원문제 정의¶
- 일주경로: 한 도시에서 출발하여 다른 모든 도시를 한 번씩만 들린 후 출발한 도시로 돌아오는 경로
- 최적일주경로: 최소거리 일주경로
- 외판원문제: 최소한 하나의 일주경로가 존재하는 가중치포함 방향그래프에서 최적일주경로 찾기
주의사항¶
- 출발하는 도시가 최적일주경로의 길이와 무관함.
- 어차피 일주경로를 따지기 때문.
- 따라서 한 지점(마디)에서 출발하는 일주경로만을 대상으로 알고리즘 구현.
예제¶
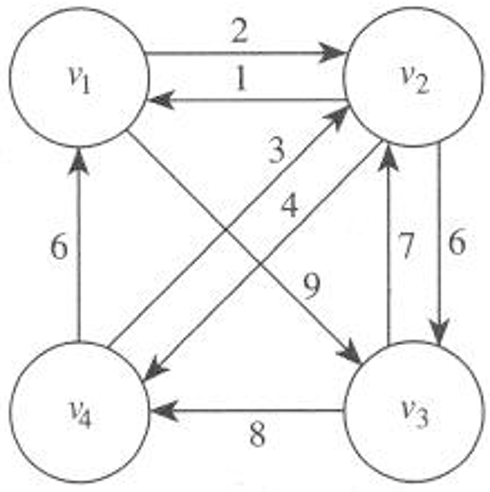
- $v_1$을 출발점으로 하는 일주경로 3개.
\begin{align*}
\textit{length}\, [v_1, v_2, v_3, v_4, v_1] &= 22 \\
\textit{length}\, [v_1, v_3, v_2, v_4, v_1] &= 26 \\
\textit{length}\, [v_1, v_3, v_4, v_2, v_1] &= 21
\end{align*}
- 마지막 경로가 최적.
무차별 대입 방식(brute force) 탐색¶
- $v_1$부터 시작하는 모든 일주경로를 확인하는 방식
부르트포스 탐색 알고리즘¶
- 도시간 거리: 중첩 사전(딕셔너리)으로 구현
- 키: 도시명
- 키값(사전 자료형)
- 키: 해당 도시와 이음선으로 연결된 도시
- 키값: 그 도시로의 이동 거리
In [1]:
from math import inf
from itertools import permutations
city_distances = {
"v1":
{"v2": 2,
"v3": 9},
"v2":
{"v1": 1,
"v3": 6,
"v4": 4},
"v3":
{"v2": 7,
"v4": 8},
"v4":
{"v1": 6,
"v2": 3}
}
- 도시명 모음
In [30]:
cities = list(city_distances.keys())
In [31]:
print(cities)
['v1', 'v2', 'v3', 'v4']
- $v_1$에서 출발하는 모든 일주경로의 순열조합
- $v_1$을 제외한 나머지 $n-1$개의 도시로 만들 수 있는 모든 순열조합
- 순열조합 수: $(n-1)!$
- $n=4$일 경우: 총 $3! = 6$개의 일주경로 존재.
- $v_1$을 제외한 나머지 $n-1$개의 도시로 만들 수 있는 모든 순열조합
- 주의: 이음선이 없는 경우가 포함된 경로는 이후 최적일주경로 선정 과정에서 제외처리될 것임.
city_permutations가 가리키는 값은 아래 6개의 항목으로 이루어진 이터러블 자료형
In [32]:
city_permutations = permutations(cities[1:])
('v2', 'v3', 'v4'),
('v2', 'v4', 'v3'),
('v3', 'v2', 'v4'),
('v3', 'v4', 'v2'),
('v4', 'v2', 'v3'),
('v4', 'v3', 'v2')
- $v_1$에서 출발하는 일주경로 완성을 위해 출발도시를 처음과 마지막 항목으로 추가
In [26]:
tsp_paths = [(cities[0],) + c + (cities[0],) for c in city_permutations]
tsp_paths는 $v_1$에서 시작하는 모든 일주경로의 목록을 담은 리스트.
[('v1', 'v2', 'v3', 'v4', 'v1'),
('v1', 'v2', 'v4', 'v3', 'v1'),
('v1', 'v3', 'v2', 'v4', 'v1'),
('v1', 'v3', 'v4', 'v2', 'v1'),
('v1', 'v4', 'v2', 'v3', 'v1'),
('v1', 'v4', 'v3', 'v2', 'v1')]
최단 일주경로 길이 확인하기¶
- $v_1$에서 출발하는 모든 일주경로를 대상으로 경로의 길이를 계산하는 단순한 코드임.
best_path: 최적일주경로 저장- 초기값은
None.
- 초기값은
best_distance: 최적일주경로의 길이 저장- 초기값은 무한대(
inf). inf: 어떤 수보다 큰 값을 나타내는 기호.
- 초기값은 무한대(
In [37]:
best_path = None
min_distance = inf
- 모든 경로를 대상으로 길이를 확인한 다음 최적일주경로의 길이를 업데이트함.
- 일주경로상에서 두 마디 사이에 이음선이 존재하지 않으면 일주경로의 길이를 무한대(
inf)로 처리함.- 이런 방식으로 실제로 존재하지 않는 일주경로를 최소거리 경쟁에서 제외시킴.
- 두 마디 사이에 이음선 존재여부 확인
- 사전 자료형의
get메서드가None을 반환하는 성질 활용
- 사전 자료형의
last와next를 차례대로 업데이트하면서 일주경로의 길이 계산last: 경로상에서 외판원의 현재 위치next: 경로상에서 외판원이 방문할 다음 위치
In [41]:
for path in tsp_paths:
distance = 0
last = path[0]
for next in path[1:]:
last2next = city_distances[last].get(next)
if last2next: # last에서 next로의 경로가 존재하는 경우
distance += last2next
else: # last에서 next로의 경로가 존재하지 않는 경우 None 반환됨.
distance = inf # 무한대로 처리하며, 결국 최솟값 경쟁에서 제외됨.
last = next
if distance < min_distance: # 최단경로를 업데이트 해야 하는 경우
min_distance = distance
best_path = path
In [40]:
print(f"최적일주경로는 {best_path}이며 길이는 {min_distance}이다.")
최적일주경로는 ('v1', 'v3', 'v4', 'v2', 'v1')이며 길이는 21이다.
- 함수로 정리하기
In [68]:
def tsp_bruteforce(city_distances:dict):
# v1에서 시작하는 모든 일주경로 확인
cities = list(city_distances.keys())
city_permutations = permutations(cities[1:])
# 최적경로와 최단길이 기억
best_path = None
min_distance = inf
# 각 일주경로의 길이확인. 동시에 최적경로와 최단길이 업데이트
for path in tsp_paths:
distance = 0
last = path[0]
for next in path[1:]:
last2next = city_distances[last].get(next)
if last2next: # last에서 next로의 경로가 존재하는 경우
distance += last2next
else: # last에서 next로의 경로가 존재하지 않는 경우 None 반환됨.
distance = inf # 무한대로 처리하며, 결국 최솟값 경쟁에서 제외됨.
last = next
if distance < min_distance: # 최단경로를 업데이트 해야 하는 경우
min_distance = distance
best_path = path
# 최적경로와 최단길이 반환
return best_path, min_distance
In [67]:
best_path, min_distance = tsp_bruteforce(city_distances)
print(f"최적일주경로는 {best_path}이며 길이는 {min_distance}이다.")
최적일주경로는 ('v1', 'v3', 'v4', 'v2', 'v1')이며 길이는 21이다.
부르트포스 탐색 시간복잡도¶
- 입력크기: 도시(마디) 수 $n$
- 단위연산: $v_1$을 제외한 나머지 $n-1$개의 도시를 일주하는 경로의 모든 경로를 고려하는 방법
$$
(n-1)(n-2)\cdots 1 = (n-1)! \in \Theta(n!)
$$
- 설명: 하나의 도시에서 출발해서
- 둘째 도시는 $(n-1)$개 도시 중 하나,
- 셋째 도시는 $(n-2)$개 도시 중 하나,
- ....
- $(n-1)$번째 도시는 $2$개 도시 중 하나,
- 마지막 $n$번째 도시는 남은 도시 하나.
더 좋은 알고리즘¶
- 외판원 문제에 대한 쉬운 해결책은 없음.
- 도시가 많은 경우 대부분의 알려진 알고리즘은 최적일주경로의 근사치를 계산함.
- 동적계획법 또는 유전 알고리즘을 이용하면 시간복잡도가 조금 더 좋은 알고리즘 구현 가능
- 하지만 모두 지수함수 이상의 복잡도를 가짐.
동적계획법으로 구현한 외판원문제 알고리즘 복잡도¶
- 일정 시간복잡도: $\Theta(n^2\, 2^n)$
- 일정 공간복잡도: $\Theta(n\, 2^n)$
- 부르트포스 알고리즘보다 훨씬 빠르기는 하지만 여전히 실용성은 없음.
- 실제로 구현하기도 쉽지 않음.
- 다양한 트릭이 있지만 알고리즘 공부에 별 도움되지 않음.
- 유전 알고리즘 기법을 활용하여 적절한 근사치를 빠르게 계산하는 알고리즘에 대한 연구가 많이 진행되어 왔음.
- 필요할 경우 가정 적절한 유전 알고리즘 활용해야 함.
다항식 시간복잡도 알고리즘은?¶
- 다항식 복잡도를 갖는 외판원문제 해결 알고리즘 알려지지 않음.
- 그런 알고리즘은 존재할 수 없다는 증명도 알려지지 않음.
- 이와같이 해답구하기가 매우 어려운 문제들에 대해 9장에서 좀 더 상세히 다룸.