3장 동적계획법

주요 내용

1편

• 1절 이항계수 구하기

• 2절 플로이드-워셜 최단경로 알고리즘

• 3절 동적계획법과 최적화 문제

2편

• 4절 외판원 문제

동적계획법

• 분할정복 알고리즘과 유사함.

• 문제의 입력사례를 분할하여 문제를 해결함

• 하지만, 작은 입력사례에 대한 결과를 기억해 두고, 나중에 필요할 때 사용한다는 점에서 분할정복과 다름.

하향식 대 상향식

• 분할정복: 하향식(top-down) 방식. 재귀 알고리즘으로 구현하기에 매우 적절함.

• 동적계획법: 상향식(bottom-up) 방식. 작은 입력사례의 결과를 기억해둔 후 필요할 때 활용.

계획(programming)의 어원

• 계획(programming)의 원래 의미: 저장용도의 배열 구현하기

• 여기서는 다양한 형태의 배열 활용법을 다룸.

1절 이항계수 구하기

파스칼의 삼각형

• 이전 행의 두 원소를 더해 새로운 원소를 추가해서 만드는 삼각형

• $n$번 행의 $k$번째 값 $a_{n, k}$에 대해 다음 점화식 성립:

  $$a_{n, k} = a_{(n-1), (k-1)} + a_{(n-1), k}$$

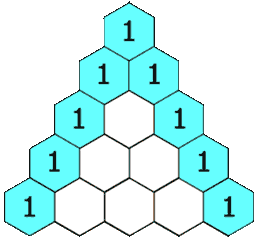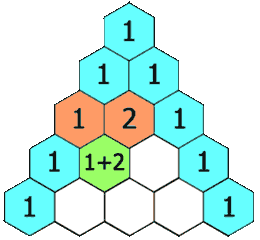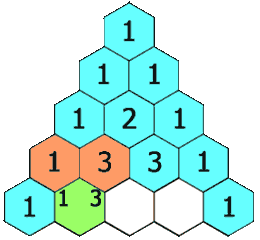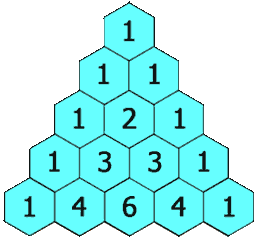
<출처: 파스칼의 삼각형(위키피디아)>

이항계수

• 파스칼의 삼각형에 사용된 값은 이항계수와 동일. 이유는 잠시 뒤 설명.

$$a_{n, k} = {n\choose k}$$

이항계수의 의미 1

• 서로 다른 $n$ 개의 구술 중에서 임의로 서로 다른 $k$개의 구술을 선택하는 방법 (단, $0 \le k \le n$).

$$ {n\choose k} = \frac{n!}{k! \, (n-k)!} $$

이항계수의 의미 2

• 아래 다항식의 계수:

\begin{align*} (x + y)^n &= b_{n,0}\, x^n\, y^0 + b_{n,1}\, x^{n-1}\, y^1 + b_{n,2}\, x^{n-2}\, y^2 + \cdots + b_{n, (n-1)}\, x^1\, y^{n-1} + b_{n,n}\, x^0\, y^n \\ &= \sum_{k=0}^{n} {n\choose k}\, x^{n-k}\, y^k \\ &= \sum_{k=0}^{n} b_{n,k}\, x^{n-k}\, y^k \end{align*}

• 응용 예제

\begin{align*} 2^n &= (1 + 1)^n \\ &= \sum_{k=0}^{n} {n \choose k}\\ &= {n\choose 0} + {n\choose 1} + {n\choose 2} + \cdots + {n\choose n-1} + {n\choose n} \end{align*}

이항계수와 파스칼의 삼각형

이항계수에 대해 아래 점화식 성립

$$ {n\choose k} = \begin{cases} {n-1 \choose k-1} + {n-1\choose k}, & 0 < k < n \\ & \\ 1, & k \in \{0, n\} \end{cases} $$

증명

• ${n \choose k}$: 1부터 $n$까지 번호가 붙은 $n$개의 구슬에서 서로 다른 $k$개의 구슬을 선택하는 방법의 수

• $k = 0$: 구슬을 전혀 선택하지 않는 하나의 방법 존재

• $k = n$: 구슬 전체를 선택하는 하나의 방법 존재

• $0 < k < n$이라고 가정. 다음 두 경우 발생

• $n$번 구슬이 선택되는 경우: 1부터 $n-1$번 까지의 구슬에서 $k-1$개의 구슬을 선택하는 방법의 수

  $${n-1 \choose k-1}$$

• $n$번 구슬이 선택되지 않는 경우: 1부터 $n-1$번 까지의 구슬에서 $k$개의 구슬을 선택하는 방법의 수

  $${n-1 \choose k}$$

• 따라서 다음 성립:

  $${n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}$$

• 2차원 행렬 형식으로 표현하면 다음과 같음.

        1
        1  1
        1  2  1
        1  3  3  1
        1  4  6  4  1
        1  5 10 10  5  1
        ...

이항계수 알고리즘 구현: 재귀 (분할정복)

• 문제: 이항계수 계산

• 입력 파라미터: 음이 아닌 정수 $n$과 $k$, 단, $k \le n$.

• 반환값: ${n \choose k}$

이항계수 재귀 알고리즘

def bin(n, k):
    # 초기값
    if k == 0 or k == n:
        return 1
    # 재귀
    else:    
        return bin(n-1, k-1) + bin(n-1, k)

• 참고: 재귀 피보나찌 수열 함수와 유사. (1장)

def fib(n):
        if (n <= 1):
            return n
        else:
            return fib(n-2) + fib(n-1)

bin 알고리즘의 복잡도

• 매우 비효율적임.

• 이유: 반복된 계산이 매우 많음. 피보나찌 수열의 경우와 유사.

• 예를 들어, bin(n-1, k-1) 과 bin(n-1, k) 는 둘 모두 서로 독립적으로 bin(n-2, k-1)를 계산함.

• bin(n, k) 계산을 위해 필요한 bin() 함수 호출 횟수 (증명 생략):

$$ 2{n\choose k} -1 $$

• 기본적으로 지수함수 정도의 나쁜 시간복잡도를 가짐. 이유:

$$ {n\choose k} \approx \frac{n^k}{k!} $$

이항계수 알고리즘 구현: 동적계획법

• 반복을 이용한 피보나찌 함수 구현에 사용된 아이디어임.

• 작은 입력사례에 대한 결과를 배열에 저장해두고 필요할 경우 재활용함.

• 아래 피보나찌 함수를 동적계획법으로 구현한 것과 유사하게 구현 가능.

def fib2(n):
        f = []

        f.append(0)
        if n > 0:
            f.append(1)
            for i in range(2, n+1):
                fi = f[i-2] + f[i-1]
                f.append(fi)
        return f[n]

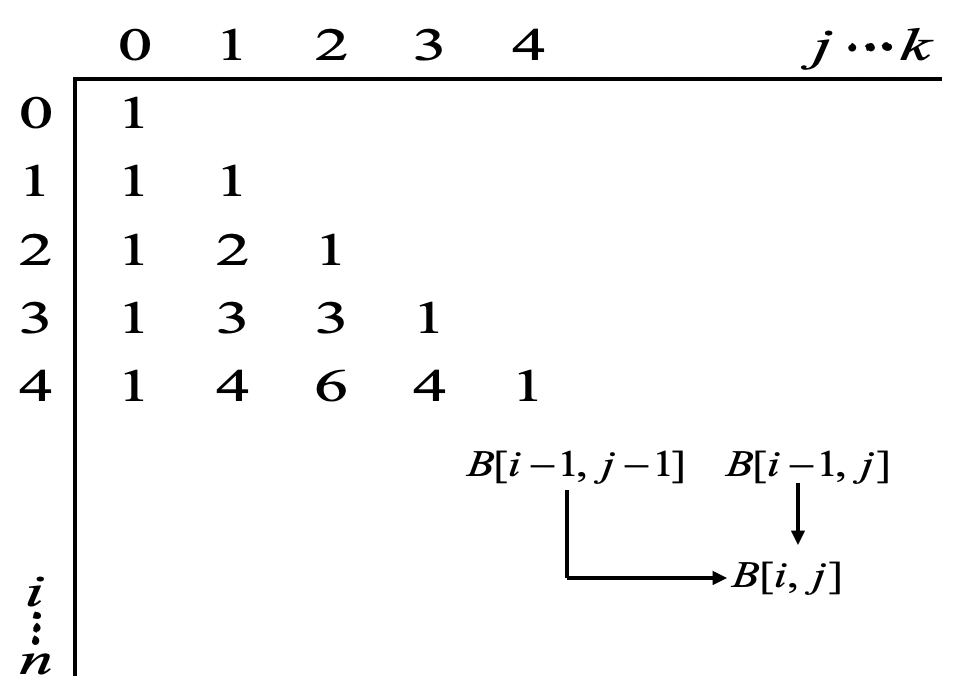
• ${n \choose k}$를 구하기 위해 아래 그림과 같이 2차원 행렬 $B$의 항목을 채워나가야 함.
  • $B[0][0]$ 에서 시작
  • 위에서 아래로 재귀 관계식을 적용하여 파스칼의 삼각형을 완성해 나가야 함.

리스트 조건제시법 활용 예제

• 일정 모양의 리스트를 생성할 때 유용함.
• 알고리즘에 사용될 행렬 $B$를 영행렬로 초기화할 때 사용.

# n = 5, k = 3 인 경우 6x4 크기의 영행렬 생성하기
# 리스트 조건제시법 활용

[[0 for _ in range(3+1)] for _ in range(5+1)]

[[0, 0, 0, 0],
 [0, 0, 0, 0],
 [0, 0, 0, 0],
 [0, 0, 0, 0],
 [0, 0, 0, 0],
 [0, 0, 0, 0]]

# 이분검색 동적계획법

def bin2(n, k):
    # n x k 모양의 행렬 준비하기.
    # 리스트 조건제시법 활용
    
    B = [[0 for _ in range(k+1)] for _ in range(n+1)]

    for i in range(n+1):
        for j in range(min(i, k) + 1):
            if j == 0 or j == i:
                B[i][j] = 1
            else:
                B[i][j] = B[i-1][j-1] + B[i-1][j]
    
    return B[n][k]

실행시간 비교

• 재귀 알고리즘과 동적계획법 알고리즘 비교

• $n=30$, $k=14$에 대해 동적계획법 알고리즘은 바로 계산

bin2(30, 14)

145422675

• 반면에 재귀 알고리즘은 30여초 이상 걸림. $n, k$가 좀 더 커지면 매우 오래 걸림.

import time

start = time.time()
bin(30,14)
end = time.time()
print(end-start)

28.078381061553955

동적계획법 알고리즘 시간복잡도

• 입력 크기: $n$과 $k$
• 단위연산: j 변수에 대한 for 반복문 실행횟수

i = 0일 때:      1회
i = 1일 때:      2회
i = 2일 때:      3회
...
i = k-1일 때:    k회
i = k일 때:      k+1회
i = (k+1)일 때:  k+1회
...
i = n일 때:      k+1회

• 따라서 다음 성립

\begin{align*} 1 + 2 + 3 + \cdots + k + (k+1)\cdot (n-k+1) &= \frac{(2n-k+2)(k+1)}{2} \\ &\in\Theta(n\,k) \end{align*}

동적계획법 알고리즘 개선하기

방법 1

• 길이가 $k+1$인 1차원 배열 이용 가능

• 이유: $i$번 행을 계산하기 위해 $i-1$번 행만 필요하기 때문.

방법 2

• 아래 사실 이용 가능

$$ {n \choose k} = {n \choose n-k} $$

• 참조: PythonTutor: 동적계획법 이항계수 알고리즘

2절 플로이드-워셜 최단경로 알고리즘

그래프 용어

• 마디 또는 정점(vertex, node)

• 이음선(edge, arc)

• 방향 그래프(directed graph, or digraph): 이음선에 방향이 포함된 그래프

• 가중치(weight)

• 가중치 포함 그래프(weighted graph)

• 경로(path): 이음선으로 연결된 마디들의 나열. 즉, 하나의 마디에서 다른 마디로 가는 이음선의 연결.

• 단순경로(simple path): 같은 마디를 두 번 지나지 않는 경로

• 순환(cycle): 하나의 마디에서 출발하여 다시 그 마디로 돌아오는 경로

• 순환 그래프(cyclic graph): 순환을 갖는 그래프

• 비순환 그래프 (acyclic graph): 순환을 갖지 않는 그래프

• 경로의 길이(length):
  • 가중치 포함 그래프의 경우: 경로 상에 있는 가중치의 합
  • 가중치 없는 그래프의 경우: 경로 상에 있는 이음선의 수

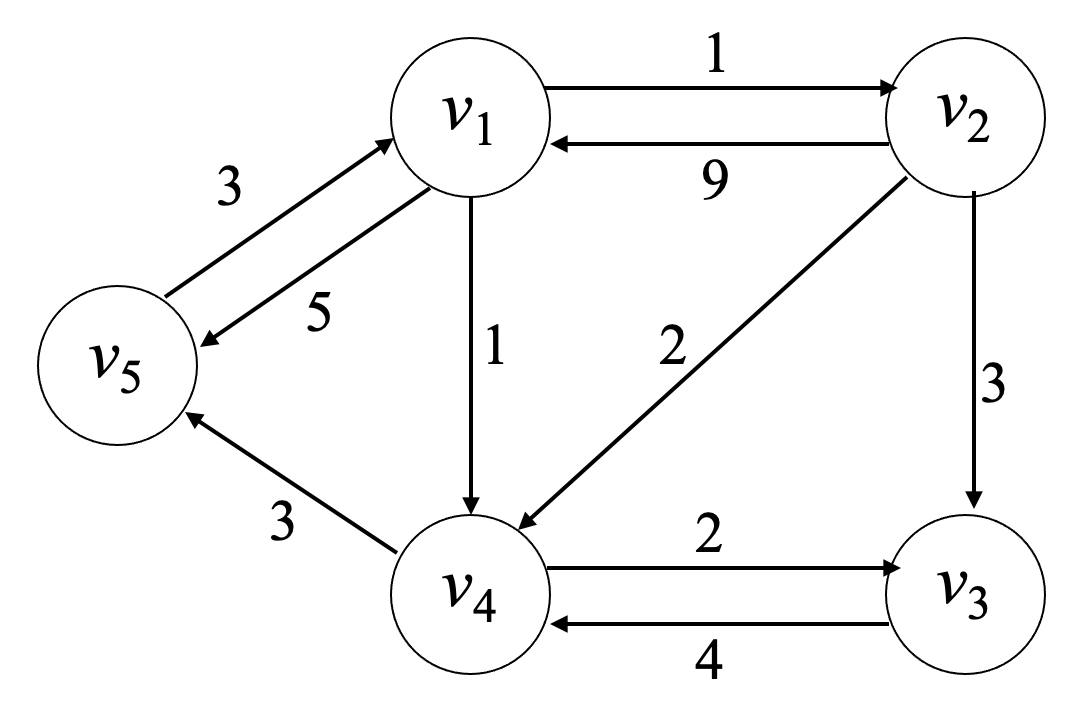
예제: 가중치 포함 방향그래프

최단경로 문제

• 임의의 하나의 마디에서 다른 임의의 마디로 가는 최단 경로 구하기

• 가중치 포함, 방향성 존중.

• 주의사항: 최단경로는 순환을 포함하지 않아야 함. 즉, 단순경로만 대상으로 삼아도 됨.

예제

• 위 그래프에서 $v_1$에서 $v_3$로 가는 단순경로와 경로 길이:
  • $[v_1, v_2, v_3]$
    • 경로 길이: $1 + 3 = 4$
  • $[v_1, v_4, v_3]$
    • 경로 길이: $1 + 2 = 3$
  • $[v_1, v_2, v_4, v_3]$
    • 경로 길이: $1 + 2 + 2 = 5$

• 따라서 최단경로와 길이는 다음과 같음.
  • $[v_1, v_4, v_3]$
    • 경로 길이: $1 + 2 = 3$

응용 사례

• 도시 간의 최단경로

• 다구간 비행기표 여정

• 지도앱에서 경유 추가

최적화 문제

• 하나 이상의 해답 중에서 최적의 값을 갖는 해답을 찾아야 하는 문제

• 최적값: 문제에 따라 최댓값 또는 최솟값을 가리킴.

• 예제: 최단경로 찾기 문제.
  • 최소 경로길이를 갖는 해답을 찾아야 함.
  • 하나의 마디에서 다른 마디로의 최단경로가 여러 개 있을 수 있음.
  • 그럴 때는 그 중에 하나 선택.

최단경로 문제 무작정 알고리즘

• 하나의 마디에서 다른 마디로의 모든 경로의 길이를 계산한 후 그 중에 최소길이 선택.

• 지수보다 나쁜 시간복잡도를 가짐.

무작정 알고리즘 분석

• 가정:
  • $n$ 개의 마디: $v_1, v_2, ..., v_n$
  • 모든 마디들 사이에 이음선 존재

• $v_1$에서 어떤 마디 $v_n$으로 가는 경로 중 나머지 모든 마디를 한 번씩 꼭 거쳐서 가는 경로들의 수는?

  • $v_1$ 에서 출발하여 처음에 도착할 수 있는 마디의 가지 수는 $(n-2)$ 개
  • 그 중에 하나를 선택하면, 그 다음에 도착할 수 있는 마디의 가지 수는 $(n-3)$개
  • ...

  • 따라서 총 경로의 개수는 다음과 같음:

    $$(n-2)\times(n-3)\times\cdots\times 1= (n-2)!$$

• 이 경로의 수만 보아도 지수보다 훨씬 큼. 따라서 실용성이 전혀 없음.

최단경로 알고리즘 동적계획법 설계 전략

그래프의 인접행렬

• 마디와 마디를 잇는 이음선과 가중치의 정보를 표현하는 2차원 행렬

• 다음과 같이 정의되는 $n\times n$ 행렬 $W$로 표현할 수 있음.

$$ W[i][j] = \begin{cases} \text{이음선 가중치} & \quad\text{$v_i$ 에서 $v_j$ 로의 이음선이 존재하는 경우} \\ \infty & \quad\text{$v_i$ 에서 $v_j$ 로의 이음선이 존재하지 않는 경우} \\ 0 & \quad \text{$i = j$ 인 경우} \end{cases} $$

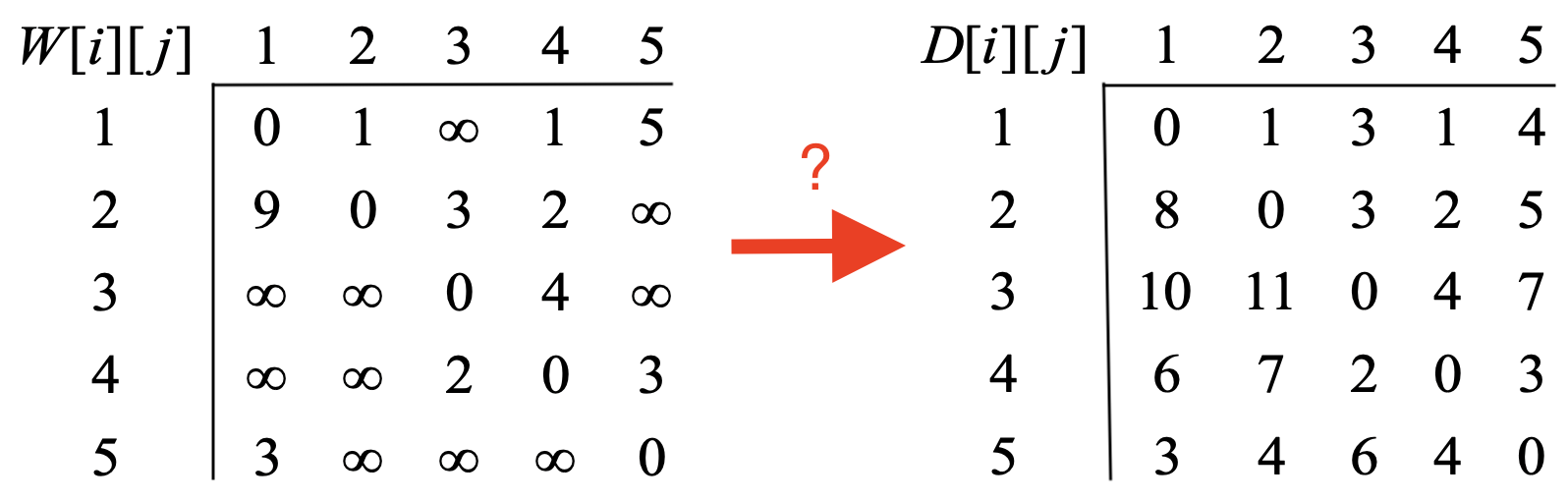
• 예제: 위 예제 그래프의 인접행렬

최단경로길이 행렬

• 각 마디들 사이의 최단경로의 길이를 담은 2차원 행렬 $D$

• 예제: 위 예제 그래프의 최단경로 길이 행렬

최단경로 길이행렬 구하기

동적계획법 전략

• 작은 입력사례 살펴보기

• $0 \le k \le n$ 를 만족하는 $k$에 대해 다음을 만족하는 2차원 행렬 $D^{(k)}$ 생성하기

\begin{align*} D^{(k)}[i][j] &= \text{집합 $\{v_1, v_2, \dots, v_k\}$ 에 속하는 마디만을 통해서} \\ & \quad\,\text{$v_i$ 에서 $v_j$ 로 가는 최단경로의 길이} \end{align*}

• 다음이 성립함.

\begin{align*} D^{(0)} &= W \\ D^{(n)} &= D \end{align*}

• 남은 과제: $D^{(k-1)}$ 로부터 $D^{(k)}$ 생성하기.

$$ D^{(0)} \longrightarrow D^{(1)}\longrightarrow D^{(2)} \longrightarrow \cdots \longrightarrow D^{(n-1)}\longrightarrow D^{(n)} $$

예제

• 위 예제 그래프에 대해 $D^{(k)}[2][5]$ 계산하기

• $D^{(0)}[2][5] = W[2][5] = \infty$

• $D^{(1)}[2][5] = \min (D^{(0)}[2][5], \text{length}[v_2, v_1, v_5]) = \min(\infty, 14) = 14$

• $D^{(2)}[2][5] = D^{(1)}[2][5] = 14$

• $D^{(3)}[2][5] = D^{(2)}[2][5] = 14$

• $D^{(4)}[2][5] = \min (D^{(3)}[2][5], d^{(4)}) = \min(14, 5) = 5$

\begin{align*} d^{(4)} &= \min(\text{length}[v_2, v_4, v_5], \text{length}[v_2, v_1, v_4, v_5], \text{length}[v_2, v_3, v_4, v_5]) \\ &= \min(5, 13, 10) \\ &= 5 \end{align*}

• $D^{(5)}[2][5] = D^{(4)}[2][5] = 5$

$D^{(k)}$ 의 재귀적 성질

• $D^{(k)}[i][j]$ 를 재귀적으로 정의할 수 있음.

$$D^{(k)}[i][j] = \min \big( D^{(k-1)}[i][j],\,D^{(k-1)}[i][k] + D^{(k-1)}[k][j] \big)$$

• 경우 1: $\{v_1, v_2,\dots, v_k\}$ 에 속한 마디들만을 통해서 $v_i$에서 $v_j$로 가는 최단경로가 $v_k$를 거쳐가지 않는 경우.

  $$D^{(k)}[i][j] = D^{(k-1)}[i][j]$$
  

  • 예제: $D^{(5)}[1][3] = D^{(4)}[1][3] = 3$

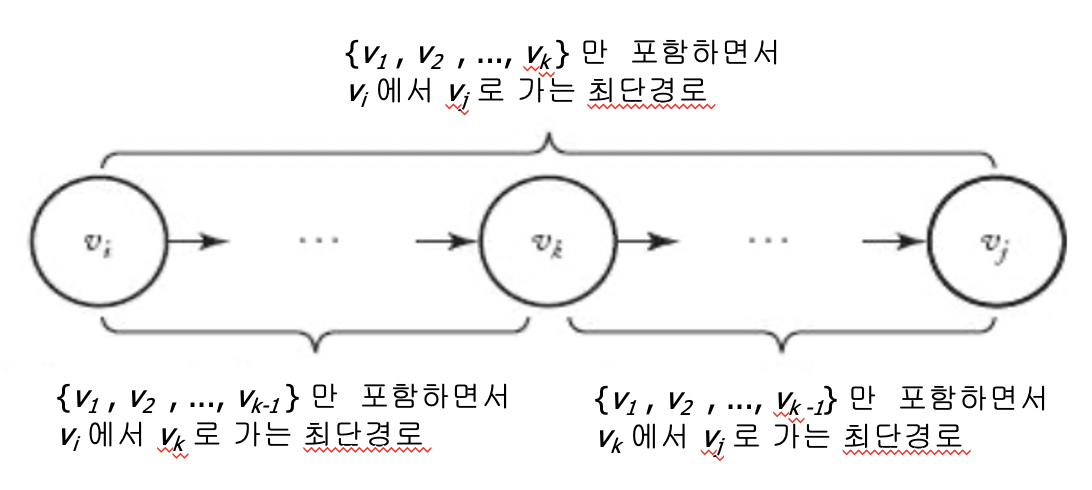
• 경우 2: $\{v_1, v_2,\dots, v_k\}$ 에 속한 마디들만을 통해서 $v_i$에서 $v_j$로 가는 최단경로가 $v_k$를 거쳐가는 경우.

  $$D^{(k)}[i][j] = D^{(k-1)}[i][k] + D^{(k-1)}[k][j]$$
  

  • 예제: $D^{(2)}[5][3] = 7 = 4 + 3 = D^{(1)}[5][2] + D^{(1)}[2][3]$

• 이유: 아래 그림 참조

플로이드-워셜 알고리즘

• 아래 화살표 과정을 구현하는 알고리즘.
• 앞서 설명한 재귀적 성질 이용

$$ W = D^{(0)} \longrightarrow D^{(1)}\longrightarrow D^{(2)} \longrightarrow \cdots \longrightarrow D^{(n-1)}\longrightarrow D^{(n)} = D $$

• 입력: 마디 수가 $n$인 가중치포함 그래프. 2차원 인접행렬로 표현됨.
• 출력: 하나의 마디에서 다른 마디로 가는 최단경로의 길이를 담은 2차원 행렬.

from copy import deepcopy

def floyd_warshall(W):
    n = len(W)

    # D^(0) 지정
    # 주의: deepcopy를 사용하지 않으면 W에 혼란을 발생시킴
    D = deepcopy(W)

    # k가 0부터 (n-1)까지 이동하면서 D가 D^(1), ..., D^(n)을 차례대로 모방함.
    # 즉, D를 업데이트하는 방식을 이용하여 최종적으로 D^(n) 생성
    for k in range(0, n):
        # 행렬의 인덱스는 0부터 (n-1)까지 이동
        for i in range(0, n):
            for j in range(0, n):
                D[i][j] = min(D[i][j] , D[i][k]+ D[k][j])
    
    # 최종 완성된 D 반환
    return D

예제

• 위 예제 그래프의 인접행렬은 다음과 같음.

# 무한에 해당하는 기호 사용
from math import inf

# inf 는 두 마디 사이에 이음선이 없음을 의미함.
W = [[0, 1, inf, 1, 5],
     [9, 0, 3, 2, inf],
     [inf, inf, 0, 4, inf],
     [inf, inf, 2, 0, 3],
     [3, inf, inf, inf, 0]]

• 플로이드-워셜 알고리즘의 결과: 앞서 살펴 본 행렬 $D$와 동일.

floyd_warshall(W)

[[0, 1, 3, 1, 4],
 [8, 0, 3, 2, 5],
 [10, 11, 0, 4, 7],
 [6, 7, 2, 0, 3],
 [3, 4, 6, 4, 0]]

• 참조: PythonTutor: 플로이드-워셜 알고리즘

최단경로 확인 알고리즘

• 이전 함수를 약간 수정하여 최단경로를 출력하는 함수 구현

추가사항

• 두 마디 사이의 최단경로에 사용된 마디 중에서 가장 큰 인덱스를 기억하는 행렬 $P$

• 즉, 다음이 성립해야 함.

$$ P[i][j] = \begin{cases} k & \text{최단경로의 중간에 사용된 마디의 인덱스 중에서 가장 큰 값이 $k$인 경우} \\ & \text{(아래 그림에서 사용된 $v_k$의 인덱스 $k$)}\\ & \\ 0 & \text{최단경로의 중간에 사용된 마디가 없는 경우} \end{cases} $$

• 나머지 사항은 동일함.

from copy import deepcopy

def floyd_warshall2(W):
    n = len(W)

    # deepcopy를 사용하지 않으면 D에 혼란을 발생시킴
    D = deepcopy(W)
    P = deepcopy(W)
    
    # P 행렬 초기화. 모든 항목을 -1로 설정
    for i in range(n):
        for j in range(n):
            P[i][j] = -1

    # k가 0부터 (n-1)까지 이동하면서 D가 D^(1), ..., D^(n)을 차례대로 모방함.
    # 그와 함께 동시에 P 행렬도 차례대로 업데이트함.
    for k in range(0, n):
        for i in range(0, n):
            for j in range(0, n):
                if D[i][k]+ D[k][j] < D[i][j]:
                    P[i][j] = k
                    D[i][j] = D[i][k]+ D[k][j]
    
    # 최종 완성된 P도 반환
    return D, P

최단경로 찍어보기: 방식 1

• 지정된 두 마디 사이의 최단경로 찍어보기
• 아래 path 함수는 두 마디 사이의 최단 경로상에 위치한 마디를 순서대로 보여줌.

def path(P, q, r):
    # 인덱스가 0부터 출발하기에 -1 또는 +1을 적절히 조절해야 함.
    if P[q-1][r-1] != -1:
        v = P[q-1][r-1]

        path(P, q, v+1)
        print(v+1,end=' ')
        path(P, v+1, r)

예제: $v_5$에서 $v_3$으로 가는 최단경로상의 중간마디 확인

• $v_1$과 $v_4$를 지나간다는 사실을 다음과 같이 확인해줌.

_, P = floyd_warshall2(W)

P

[[-1, -1, 3, -1, 3],
 [4, -1, -1, -1, 3],
 [4, 4, -1, -1, 3],
 [4, 4, -1, -1, -1],
 [-1, 0, 3, 0, -1]]

path(P, 5, 3)

1 4 

• 참조: PythonTutor: 최단경로 확인하기 1

최단경로 찍어보기: 방식 2

• 최단경로 상에 위치한 마디를 리스트로 담을 수 있음.

def path2(P, q, r, route):
    # 인덱스가 0부터 출발하기에 -1 또는 +1을 적절히 조절해야 함.
    if P[q-1][r-1] != -1:
        v = P[q-1][r-1]

        path2(P, q, v+1, route)
        route.append(v+1)
        path2(P, v+1, r, route)
        
    return route

path2(P, 5, 3, [])

[1, 4]

• 참조: PythonTutor: 최단경로 확인하기 2

• 위 결과를 이용하여 경로를 보다 예쁘게 출력할 수 있음.

def print_path2(P, i, j):
    route = path2(P, i, j, [])
    route.insert(0, i)
    route.append(j)
    print(" -> ".join([str(v) for v in route]))

print_path2(P, 5, 3)

5 -> 1 -> 4 -> 3

print_path2(P, 2, 5)

2 -> 4 -> 5

최단경로 찍어보기: 방식 3

$$ P[i][j] = \begin{cases} k & \text{최단경로상의 마디 중에서 $v_i$에 가장 가까운 마디의 인덱스가 $k$인 경우} \\ & \\ 0 & \text{최단경로의 중간에 사용된 마디가 없는 경우} \end{cases} $$

from itertools import product

def floyd_warshall3(W):
    n = len(W)

    D = deepcopy(W)
    P = [[0]   * n for i in range(n)]
    
    for i, j in product(range(n), repeat=2):
        if 0 < W[i][j] < inf:
            P[i][j] = j
    
    for k, i, j in product(range(n), repeat=3):
        sum_ik_kj = D[i][k] + D[k][j]
        if D[i][j] > sum_ik_kj:
            D[i][j] = sum_ik_kj
            P[i][j]  = P[i][k]
    return D, P

def path3(D, P, i, j):
    # 인덱스가 0부터 출발하기에 -1 또는 +1을 적절히 조절해야 함.
        path = [i-1]
        while path[-1] != j-1:
            path.append(P[path[-1]][j-1])
        route = ' → '.join(str(p + 1) for p in path)
        print(f"최단길이:{D[i-1][j-1]:>2}, 최단경로: {route}")

D, P = floyd_warshall3(W)

path3(D, P, 5, 3)

최단길이: 6, 최단경로: 5 → 1 → 4 → 3

path3(D, P, 2, 5)

최단길이: 5, 최단경로: 2 → 4 → 5

3절 동적계획법과 최적화 문제

동적계획법에 의한 설계 절차

• 문제의 입력에 대해 최적의 해답을 제공하는 재귀 관계식 설정

• 상향식으로 최적의 해답을 계산

• 상향식으로 최적의 해답을 구축

최적의 원칙

• 어떤 문제의 입력사례에 대한 최적의 해가 그 입력사례를 분할한 모든 부분사례에 대한 최적의 해를 포함하고 있으면, 그 문제는 최적의 원칙이 적용된다 라고 말함.

• 최적의 원칙이 적용되는 문제는 동적계획법으로 해결할 수 있음.

예제: 최단경로 문제

• $v_k$를 $v_i$에서 $v_j$로 가는 최적경로 상의 마디라고 하면, $v_i$에서 $v_k$ 로 가는 부분경로와 $v_k$에서 $v_j$로 가는 부분경로도 반드시 최적이어야 함.

최적의 원칙이 적용되지 않는 예제

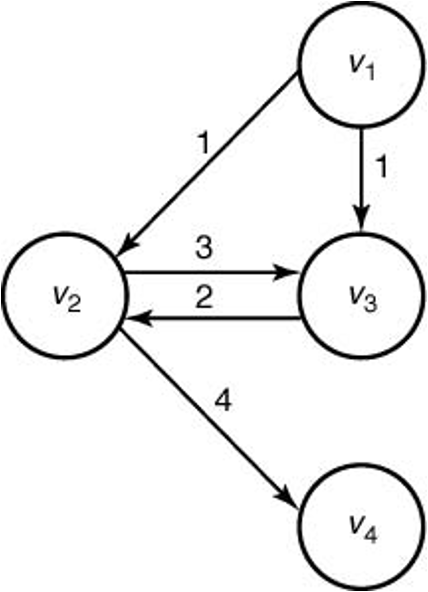
• $v_1$에서 $v_4$로의 (순환이 없는) 최장경로는 $[v_1, v_3, v_2, v_4]$ 가 된다.

• 그러나 이 경로의 부분 경로인 $v_1$에서 $v_3$으로의 (순환이 없는) 최장경로는 $[v_1, v_3]$이 아니고, $[v_1, v_2, v_3]$ 이다.

• 따라서 최적의 원칙이 적용되지 않는다.