4절 퀵정렬(분할교환정렬)

• 호어(Hoare)가 1962년에 개발

• 합병정렬과 비슷

  • 입력 리스트를 보다 작은 두 개의 리스트로 분할
  • 각각의 보다 작은 리스트를 재귀적으로 정렬

• 분할 방식

  • 기준원소(pivot) 선정
  • 기준원소보다 작은 값은 모두 리스트 왼쪽으로 이동
  • 기준원소보다 큰 값은 모두 리스트 오른쪽으로 이동

• 기준원소

  • 보통 맨 왼편에 위치한 값 선정
  • 무엇을 선택해도 확률적으로 동일함.

• 항상 가장 빠른 정렬 알고리즘은 아니지만 평균적으로 가장 빠름.

퀵정렬 작동 예제

• 정렬 대상: 15 22 13 27 12 10 20 25

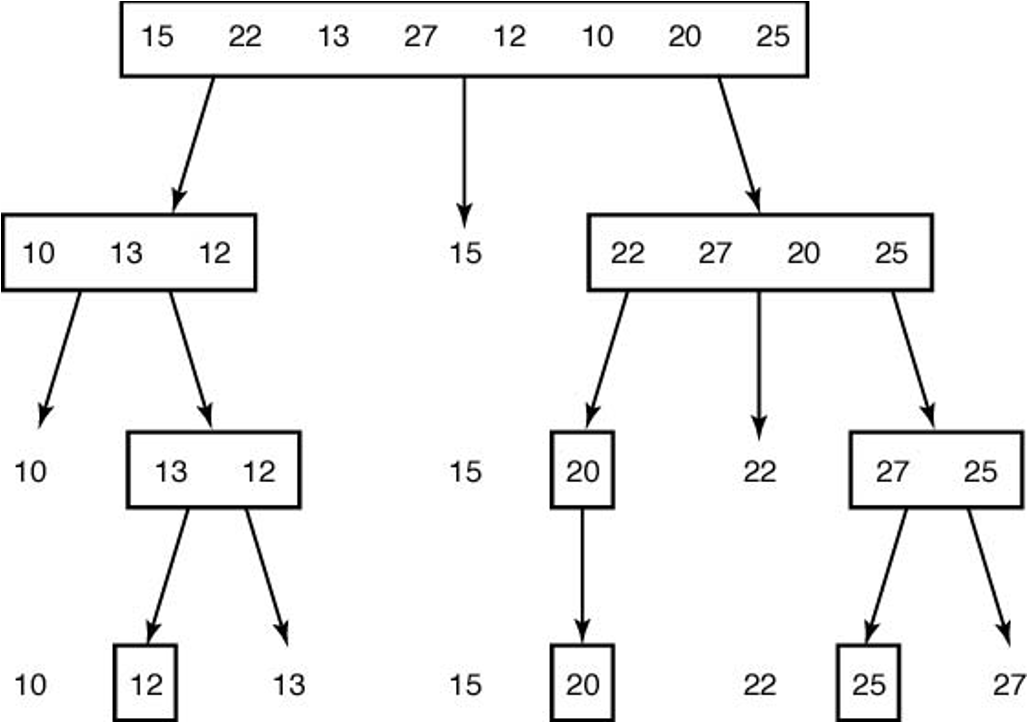
파이썬 구현: 퀵정렬 재귀

분할 알고리즘

# 분할 알고리즘: 기준원소(pivot)를 사용하여 리스트 분할하기
# 기준원소: 리스트의 맨 왼편에 위치한 값
# 주의: 리스트의 항목을 직접 수정함. 따라서 제자리 분할임.


def partition(aList, low, high):

    pivotitem = aList[low]     # 기준원소(pivot)
    pivotpoint = low           # 분할 후 기준원소가 저장될 위치
 
    # 기준원소 보다 작은 값을 리스트 왼편에 위치시키기
    # i 는 기준원소를 제외한 구간 내 항목 전체를 대상으로 움직임

    for i in range(low+1, high+1):
        if aList[i] < pivotitem:
            pivotpoint += 1
            aList[i], aList[pivotpoint] = aList[pivotpoint], aList[i]
    
    # 분할이 완료된 후 기준원소를 적절한 위치(pivotpoint)로 옮기기
    aList[low], aList[pivotpoint] = aList[pivotpoint], aList[low]
    return pivotpoint

기준원소 분할 예제

aList = [15, 22, 13, 27, 12, 10, 20, 25]
n = len(aList)

partition(aList, 0, n-1)
print(aList)

[10, 13, 12, 15, 22, 27, 20, 25]

• 참조: PythonTutor: 분할 알고리즘, 기준원소 사용

퀵정렬 알고리즘(재귀)

# 퀵정렬 재귀

# 주의: 리스트의 항목을 직접 수정함. 따라서 제자리 정렬임.

def quickSort(aList, low, high):
    if low < high:
        # 분할 후 기준원소 위치 확인
        pivotpoint = partition(aList, low, high)

        # 분할된 부분 정렬(재귀)
        quickSort(aList, low, pivotpoint-1)
        quickSort(aList, pivotpoint+1, high)
        
    return aList

퀵정렬 예제

quickSort(aList, 0, n-1)

[10, 12, 13, 15, 20, 22, 25, 27]

• 참조: PythonTutor: 퀵정렬 재귀

일정 시간복잡도 분석: 분할(partition) 알고리즘

일정 시간복잡도 $T(n)$

• 입력크기($n$): 정렬대상 조사구간 크기
• 단위연산: 기준원소(pivot)와의 비교 횟수

• 첫째 원소(기준원소)를 제외한 모든 원소와 비교. 따라서 다음 성립:

  $$T(n) = n-1$$

최악 시간복잡도 분석: 퀵정렬(quicksort) 알고리즘

• 입력크기($n$): 정렬대상 리스트 구간 크기
• 단위연산: partition 함수 실행 과정에서 기준원소(pivot)와의 비교 횟수

이미 오름차순으로 정렬된 리스트 정렬 시간 복잡도

• 이미 오름차순으로 정렬된 리스트를 정렬할 때의 시간 복잡도 $T(n)$ 계산

• 맨 왼편에 위치한 기준원소가 항상 제일 작은 값이라서 분할 후 기준원소 왼편에 위치할 리스트는 공리스트. 따라서:

\begin{align*} T(n) &= T(0) + T(n-1) + (n-1) \\ &= T(n-1) + (n-1) \\ & \\ T(0) &= 0 \end{align*}

• 위 점화식을 풀면 다음이 성립:

$$T(n) = \frac{n(n-1)}{2}$$

• 증명:

\begin{align*} T(n) &= T(n-1) + (n-1) \\ &= T(n-2) + (n-2) + (n-1) \\ &= \cdots \\ &= T(1) + 1 + 2 + \cdots + (n-1) \\ &= T(0) + 0 + 1 + \cdots + (n-1) \\ & = \frac{n(n-1)}{2} \end{align*}

최악 시간복잡도 $W(n)$

• 아래 부등식 증명 가능.

$$W(n) \le \frac{n(n-1)}{2}$$

• 증명: 귀납법 활용(생략)

• 결론

$$W(n) = \frac{n(n-1)}{2} \in \Theta(n^2)$$

평균 시간복잡도 분석: 퀵정렬(quicksort) 알고리즘

• 입력크기($n$): 정렬대상 리스트 길이
• 단위연산: partition 함수 실행 과정에서 기준원소(pivot)와의 비교 횟수

가정

• 배열의 원소가 무작위적으로 흩어져 있음.
• 따라서 기준원소의 위치(pivotpoint)가 동일한 확률 $1/n$으로 0부터 $(n-1)$ 사이의 임의의 값이 됨.

기준원소의 위치가 $p$인 경우

• 길이가 각각 $p$과 $(n-p-1)$인 부분배열로 나뉘어짐.
• 따라서 정렬을 위해 평균적으로 아래 시간이 걸릴것으로 예상됨:

$$\frac{1}{n}\, \big[ A(p) + A(n-p-1) \big]$$

• $\frac 1 n$은 기준원소의 위치가 $p$일 확률.

평균 시간복잡도 $A(n)$

• 앞서 구한 식을 임의의 $p$에 대해서 구해 더하면 평균 시간복잡도가 됨.

\begin{align*} A(n) &= \sum_{p=0}^{n-1} \frac{1}{n}\, \big[ A(p) + A(n-p-1) \big] + (n-1) \end{align*}

• $(n-1)$은 분할에 걸리는 시간을 가리킴.

• 위 식을 정리하면 다음과 같음(증명 생략).

\begin{align*} A(n) &\approx 1.38(n+1) \lg n \in \Theta(n\, \lg n) \end{align*}

5절 슈트라센의 행렬곱셈 알고리즘

• 행렬곱셈의 정의는 매우 간단함.
• 하지만 행렬의 크기가 커짐에 따라 매우 오랜 시간 소요됨.
• 이유: 두 개의 $n \times n$ 행렬 곱셈에 대한 시간복잡도는 $\Theta(n^3)$임.
  • 입력크기: 정방행렬의 행의 개수 $n$
  • 단위연산: 곱셈

표준 행렬곱셈 정의

• 일반적으로 알려진 행렬곱셈의 정의는 다음과 같음:

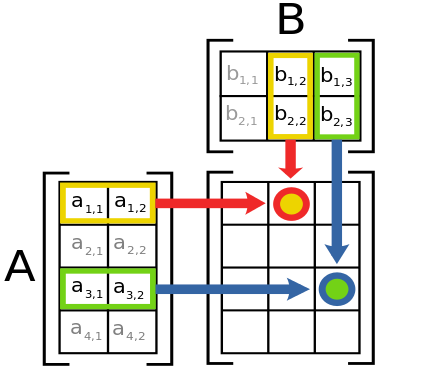
<출처: 위키피디아 - 행렬곱셈>

예제

행렬 $A$와 $B$가 아래와 같이 주어졌을 때,

$$ A = \begin{bmatrix} a_{1 1} & a_{1 2}\\ a_{2 1} & a_{2 2} \end{bmatrix} \qquad B = \begin{bmatrix} b_{1 1} & b_{1 2}\\ b_{2 1} & b_{2 2} \end{bmatrix} $$

두 행렬의 곱 $C$을 정의할 수 있다.

$$ C = A \times B = \begin{bmatrix} c_{1 1} & c_{1 2}\\ c_{2 1} & c_{2 2} \end{bmatrix} $$

이때 다음이 성립한다.

\begin{align*} c_{i j} &= a_{i 1} \cdot b_{1 j} + a_{i 2} \cdot b_{2 j} \\ &= \sum_{k=1}^{2} a_{i k} \cdot b_{k j} \end{align*}

예를 들어

\begin{align*} \begin{bmatrix} 2 & 3 \\ 4 & 1 \end{bmatrix} \times \begin{bmatrix} 5 & 7 \\ 6 & 8 \end{bmatrix} &= \begin{bmatrix} 2\times 5 + 3\times 6 & 2 \times 7 + 3 \times 8 \\ 4 \times 5 + 1 \times 6 & 4 \times 7 + 1 \times 8 \end{bmatrix} \\ &= \begin{bmatrix} 28 & 38 \\ 26 & 36 \end{bmatrix} \end{align*}

표준 행렬곱셈 일반화

• 두 개의 $n \times n$ 행렬곱셈 결과

\begin{align*} c_{i j} &= a_{i 1} \cdot b_{1 j} + a_{i 2} \cdot b_{2 j} + \cdots + a_{i n} \cdot b_{n j} \\ &= \sum_{k=1}^{n} a_{i k} \cdot b_{k j} \end{align*}

표준 행렬곱셈 알고리즘

A = [[2, 3],
     [4, 1]]

B = [[5, 7],
     [6, 8]]

C = [[0, 0],
     [0, 0]]

for i in range(0,2):
    for j in range(0, 2):
        for k in range(0, 2):
            C[i][j] += A[i][k] * B[k][j]

C

[[28, 38], [26, 36]]

def matrixmult(A, B):
    n = len(A)
    
    # C 행렬을 초기화 하기 위해 리스트 조건제시법 활용
    C = [[0 for _ in range(n)] for _ in range(n)]

    for i in range(0,2):
        for j in range(0, 2):
            for k in range(0, 2):
                C[i][j] += A[i][k] * B[k][j]
    
    return C

matrixmult(A, B)

[[28, 38], [26, 36]]

리스트 조건제시법으로 좀 더 단순하게 정의할 수 있음.

def matrixmult_com(A, B):
    n = len(A)
    C = [[sum([A[i][k] * B[k][j] for k in range(n)]) for j in range(n)] for i in range(n)]
    return C

matrixmult_com(A, B)

[[28, 38], [26, 36]]

넘파이 활용

• 넘파이 어레이의 인덱싱, 슬라이싱 기능이 탁월함.
• 기본 리스트를 이용할 경우 훨씬 많은 수고를 써야 함.

import numpy as np

def matrixmult_np(A, B):
    n = len(A)
    
    # (nxn) 크기의 0행렬 생성. 실수가 아닌 정수 행렬 생성.
    C = np.zeros((n,n), dtype=int)

    for i in range(0,2):
        for j in range(0, 2):
            for k in range(0, 2):
                C[i, j] += A[i, k] * B[k, j]
    
    return C

A1 = np.array(A)
B1 = np.array(B)

matrixmult_np(A1, B1)

array([[28, 38],
       [26, 36]])

표준 행렬곱셈의 일정 시간복잡도 분석

곱셈 기준

• 입력크기: 정방행렬의 행의 수 $n$
• 단위연산: 가장 안쪽에 있는 for 반복문에서 사용된 곱셈

• 총 곱셈 횟수:

$$ T(n) = n \times n \times n = n^3 \in \Theta(n^3) $$

덧셈 기준

• 입력크기: 정방행렬의 행의 수 $n$
• 단위연산: 가장 안쪽에 있는 for 반복문에서 사용된 덧셈

• 총 덧셈 횟수:

$$ T(n) = n \times n \times (n-1) = n^3 - n^2 \in \Theta(n^3) $$

슈트라쎈 행렬곱셈

행렬 $A$와 $B$가 아래와 같이 주어졌을 때,

$$ A = \begin{bmatrix} a_{1 1} & a_{1 2}\\ a_{2 1} & a_{2 2} \end{bmatrix} \qquad B = \begin{bmatrix} b_{1 1} & b_{1 2}\\ b_{2 1} & b_{2 2} \end{bmatrix} $$

다음이 성립한다.

$$ C = A \times B = \begin{bmatrix} m_1 + m_4 - m_5 + m_7 & m_3 + m_5\\ m_2 + m_4 & m_1 + m_3 - m_2 + m_6 \end{bmatrix} $$

\begin{align*} m_1 &= (a_{1 1} + a_{2 2})\, (b_{1 1} + b_{2 2}) \\ m_2 &= (a_{2 1} + a_{2 2})\, b_{1 1}\\ m_3 &= a_{1 1}\, (b_{1 2} - b_{2 2})\\ m_4 &= a_{2 2}\, (b_{2 1} - b_{1 1})\\ m_5 &= (a_{1 1} + a_{1 2})\, b_{2 2}\\ m_6 &= (a_{2 1} - a_{1 1})\, (b_{1 1} + b_{1 2})\\ m_7 &= (a_{1 2} - a{2 2})\, (b_{2 1} + b_{2 2}) \end{align*}

슈트라쎈의 $2\times 2$ 행렬곱셈 시간복잡도

• 슈트라쎈 행렬곱셈에 필요한 연산:
  • 곱셈: 7번
  • 덧셈/뺄셈: 18번

• 표준 행렬곱셈에 필요한 연산:
  • 곱셈: 8번
  • 덧셈/뺄셈: 4번

슈트라쎈 행렬곱셈 일반화

• 가정:

$$n = 2^k$$

• $A$와 $B$ 두 행렬을 각각 4개의 아래와 같이 부분행렬로 나눔.

$$ A = \begin{bmatrix} A_{1 1} & A_{1 2}\\ A_{2 1} & A_{2 2} \end{bmatrix} \qquad B = \begin{bmatrix} B_{1 1} & B_{1 2}\\ B_{2 1} & B_{2 2} \end{bmatrix} $$

• 이제 $C$를 다음과 같이 계산할 수 있음.

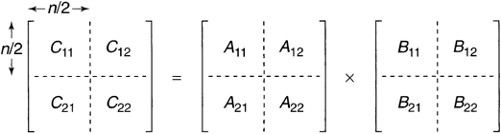
• 여기에 슈트라쎈 행렬곱셈 적용:

$$ C = A \times B = \begin{bmatrix} M_1 + M_4 - M_5 + M_7 & M_3 + M_5\\ M_2 + M_4 & M_1 + M_3 - M_2 + M_6 \end{bmatrix} $$

\begin{align*} M_1 &= (A_{1 1} + A_{2 2})\times (B_{1 1} + B_{2 2}) \\ M_2 &= (A_{2 1} + A_{2 2})\times B_{1 1}\\ M_3 &= A_{1 1}\times (B_{1 2} - B_{2 2})\\ M_4 &= A_{2 2}\times (B_{2 1} - B_{1 1})\\ M_5 &= (A_{1 1} + A_{1 2})\times B_{2 2}\\ M_6 &= (A_{2 1} - A_{1 1})\times (B_{1 1} + B_{1 2})\\ M_7 &= (A_{1 2} - a{2 2})\times (B_{2 1} + B_{2 2}) \end{align*}

슈트라쎈 행렬곱셈 파이썬 알고리즘

• numpy 모듈의 array 활용
• 그렇지 않으면 행렬 분할(partition)과 행렬 합병을 구현하기가 매우 불편해짐.

행렬 분할 알고리즘

• $n \times n$ 행렬을 크기가 절반인 네 개의 부분행렬로 분할하기

import numpy as np 

def partition(matrix): 
    """ 
    (n x n) 크기의 행렬을 (n/2 x n/2) 크기의 행렬 4개로 분할하기
    """
    size = len(matrix)
    size2 = size//2
    return (matrix[:size2, :size2], matrix[:size2, size2:], 
            matrix[size2:, :size2], matrix[size2:, size2:])

슈트라쎈 알고리즘

# 분할정복을 활용한 슈트라센의 행렬곱셈 (재귀)

def strassen(A, B): 
    # n=2 일 경우: 일반 정의가 좀 더 빠름
    if len(A) == 1: 
        return A * B

    # 행렬 인자 4등분하기. 재귀적으로 (2x2) 행렬이 만들어질 때까지.
    A11, A12, A21, A22 = partition(A) 
    B11, B12, B21, B22 = partition(B) 

    # 분할된 부분행렬에 대해 재귀 적용
    M1 = strassen(A11 + A22, B11 + B22) 
    M2 = strassen(A21 + A22, B11) 
    M3 = strassen(A11, B12 - B22) 
    M4 = strassen(A22, B21 - B11) 
    M5 = strassen(A11 + A12, B22) 
    M6 = strassen(A21 - A11, B11 + B12) 
    M7 = strassen(A12 - A22, B21 + B22) 

    # 4개의 부분행렬 완성
    C11 = M1 + M4 - M5 + M7 
    C12 = M3 + M5 
    C21 = M2 + M4 
    C22 = M1 + M3 - M2 + M6 

    # 4개의 부분행렬을 하나의 행렬로 합병
    C = np.vstack((np.hstack((C11, C12)), np.hstack((C21, C22)))) 

    return C

A2 = np.array([[1, 2, 3, 4],
              [5, 6, 7, 8],
              [9, 1, 2, 3],
              [4, 5, 6, 7]])

B2 = np.array([[8, 9, 1, 2],
              [3, 4, 5, 6],
              [7, 8, 9, 1],
              [2, 3, 4, 5]])

strassen(A2, B2)

array([[ 43,  53,  54,  37],
       [123, 149, 130,  93],
       [ 95, 110,  44,  41],
       [103, 125, 111,  79]])

• 참조: PythonTutor: 슈트라쎈 행렬곱셈 작동 예제

슈트라쎈 행렬곱셈의 일정 시간복잡도 분석

곱셈 기준

• 입력크기: 정방행렬의 행의 수 $n = 2^k$
• 단위연산: 곱셈 호출 횟수

• 총 곱셈 횟수:

\begin{align*} T(n) &= 7\, T \big(\frac n 2 \big) \\ T(1) &= 1 \end{align*}

이 식을 전개하면:

\begin{align*} T(n) &= 7\, T(2^{k-1}) \\ &= 7^2\, T(2^{k-2}) \\ &= \dots \\ &= 7^k T(1)\\ &= 7^k \\ &= 7^{\lg n} = n^{\lg 7} \\ &\approx n^{2.81} \\ &\in \Theta(n^{2.81}) \end{align*}

덧셈/뺄셈 기준

• 입력크기: 정방행렬의 행의 수 $n = 2^k$
• 단위연산: 덧셈/뺄셈 호출 횟수

• 총 덧셈/뺄셈 횟수:

\begin{align*} T(n) &= 7\, T \big( \frac n 2 \big) + 18 \big( \frac n 2 \big)^2\\ T(1) &= 0 \end{align*}

이 식을 전개하면:

\begin{align*} T(n) &= 6 n^{\lg 7} -6 n^{2} \\ &\approx 6 n^{2.81} - 6 n^2 \\ &\in \Theta(n^{2.81}) \end{align*}

$n = 2^k$가 아닌 경우

• 0으로 이루어진 행과 열을 필요한 만큼 추가하여 $2^k$ 모양의 행렬로 만든 후 슈트라쎈 알고리즘 적용
• 이후 0으로 이루어진 행과 열 삭제.
• 따라서 시간복잡도는 $\Theta(n^{2.81})$로 동일함.

표준 알고리즘 대 슈트라센 알고르즘

	표준 알고리즘	슈트라쎈 알고리즘
곱셉	$n^3$	$n^{2.81}$
덧셈/뺄셈	$n^3 - n^2$	$6 n^{2.81} - 6 n^2$

기타 알고리즘

• 슈트라센 알고리즘보다 효율적인 알고리즘은 아직 알려지지 않았음.

• 이론상: 모든 행렬곱셈 알고리즘의 복잡도는 $\Theta(n^2)$ 이상이어야 함.

• 하지만: 아직 $\Theta(n^2)$의 시간복잡도를 갖는 알고리즘은 알려지지 않았으며, 불가능하다는 증명도 없음.

8절 분할정복을 사용할 수 없는 경우

경우 1

• 크기가 $n$인 입력이 2개 이상의 조각으로 분할되며, 분할된 부분들의 크기가 거의 $n$에 가깝게 되는 경우
• 시간복잡도: 지수 시간

• 예제: 1장에서 살펴본 피보나찌 수열 계산 함수(재귀)

  fib(k) = fib(k-2) + fib(k-1)
  

경우 2

• 크기가 $n$인 입력이 거의 $n$개의 조각으로 분할되며, 분할된 부분의 크기가 $n/c$인 경우. 단, $c$는 상수.
• 시간복잡도: $n^{\Theta(\lg n)}$

• 예제:

  \begin{align*} T(n) &= n\, T(n/c) \end{align*}

연습문제

지수 시간복잡도 문제: 하노이탑

• 연습문제 17번 참조

문제

• 말뚝 3개와 크기가 모두 다른 구멍난 디스크 $n$개가 주어졌음.
• 한 말뚝에 쌓여 있는 $n$개의 디스크를 다른 말뚝으로 옮겨여 함.

제한 조건

1. 세 개의 말뚝 이외에는 디스크를 놓을 수 없음.
2. 한 번에 하나의 디스크만 옮길 수 있음.
3. 큰 디스크를 작은 디스크 위에 올려놓을 수 없음.

작동법 참조

• About the Towers of Hanoi: 직접 실행 가능

해결책 1

• 의사코드 수준의 재귀 알고리즘.
• 하지만 알고리즘 핵심은 모두 포함됨.

def pseudo_hanoi(begin, end, temp, n): 
    if n==1: 
        print(f"{begin}에서 디스크 1개를 {end}로 옮기세요")
        return

    pseudo_hanoi(begin, temp, end, n-1) 
    print(f"{begin}에서 디스크 {n}을 {end}로 옮기세요")
    pseudo_hanoi(temp, end, begin, n-1) 

# 디스크 1개
num_disks = 1

pseudo_hanoi('말뚝 A','말뚝 C','말뚝 B', num_disks) 

말뚝 A에서 디스크 1개를 말뚝 C로 옮기세요

# 디스크 3개
num_disks = 3

pseudo_hanoi('말뚝 A','말뚝 C','말뚝 B', num_disks) 

말뚝 A에서 디스크 1개를 말뚝 C로 옮기세요
말뚝 A에서 디스크 2을 말뚝 B로 옮기세요
말뚝 C에서 디스크 1개를 말뚝 B로 옮기세요
말뚝 A에서 디스크 3을 말뚝 C로 옮기세요
말뚝 B에서 디스크 1개를 말뚝 A로 옮기세요
말뚝 B에서 디스크 2을 말뚝 C로 옮기세요
말뚝 A에서 디스크 1개를 말뚝 C로 옮기세요

pseudo_hanoi의 일정 시간복잡도

• 입력크기: 디스크 수 $n$
• 단위연산: 이동 횟수

• 이동할 때 마다 카운트를 세면 됨. 따라서 아래 점화식 성립:

\begin{align*} T(n) &= T(n-1) + 1 + T(n-1) \\ &= 2\, T(n-1) + 1 \\ & \\ T(1) &= 1 \end{align*}

• 따라서 다음 성립:

\begin{align*} T(n) &= T(n-1) + 1 + T(n-1) \\ &= 2\, T(n-1) + 1 \\ &= 2^2\, T(n-2) + 2 + 1 \\ &= \dots \\ &= 2^{n-1}\, T(1) + 2^{n-2} + 2^{n-3} + \cdots + 2 + 1\\ &= 2^{n-1} + 2^{n-2} + 2^{n-3} + \cdots + 2 + 1\\ &= 2^n - 1 \end{align*}

• 이동횟수 확인을 위해 count 변수 활용 가능

def pseudo_hanoi_(begin, end, temp, n): 
    count = 0
    if n==1: 
        print(f"{begin}에서 디스크 1개를 {end}로 옮기세요")
        return count+1

    count += pseudo_hanoi_(begin, temp, end, n-1) 
    print(f"{begin}에서 디스크 {n}을 {end}로 옮기세요")
    count += 1
    count += pseudo_hanoi_(temp, end, begin, n-1) 
    
    return count

# 디스크 4개
num_disks = 4

pseudo_hanoi_('말뚝 A','말뚝 C','말뚝 B', num_disks) 

말뚝 A에서 디스크 1개를 말뚝 B로 옮기세요
말뚝 A에서 디스크 2을 말뚝 C로 옮기세요
말뚝 B에서 디스크 1개를 말뚝 C로 옮기세요
말뚝 A에서 디스크 3을 말뚝 B로 옮기세요
말뚝 C에서 디스크 1개를 말뚝 A로 옮기세요
말뚝 C에서 디스크 2을 말뚝 B로 옮기세요
말뚝 A에서 디스크 1개를 말뚝 B로 옮기세요
말뚝 A에서 디스크 4을 말뚝 C로 옮기세요
말뚝 B에서 디스크 1개를 말뚝 C로 옮기세요
말뚝 B에서 디스크 2을 말뚝 A로 옮기세요
말뚝 C에서 디스크 1개를 말뚝 A로 옮기세요
말뚝 B에서 디스크 3을 말뚝 C로 옮기세요
말뚝 A에서 디스크 1개를 말뚝 B로 옮기세요
말뚝 A에서 디스크 2을 말뚝 C로 옮기세요
말뚝 B에서 디스크 1개를 말뚝 C로 옮기세요

15

• 참조

$$ 15 = 2^4 -1 $$

해결책 2

• 말뚝에 실제로 쌓이는 것까지 구현하기
• 말뚝을 리스트로 구현
• 주의사항
  • 큰 숫자가 먼저 들어오지만, 작은 숫자가 먼저 나가는 기능을 구현해야 함.
  • 아이디어: 스택처럼 작동하도록 해야함.
    • 스택(stack): FILO(First In Last Out)를 따르는 자료구조
  • 리트스 자료형의 pop()과 append() 메서드 활용

# 말뚝 인자로 리스트 활용

def hanoi_list(begin, end, temp, n):
    if n == 1: 
        end.append(begin.pop())
    else:
        hanoi_list(begin, temp, end, n - 1) 
        hanoi_list(begin, end, temp, 1) 
        hanoi_list(temp, end, begin, n - 1)

tower_a = []
tower_b = []
tower_c = []

# 디스크 수
num_discs = 3

for i in range(num_discs, 0, -1):
    tower_a.append(i)

# 시작할 때
print("시작할 때:")
print(f"tower_a: {tower_a}")
print(f"tower_b: {tower_b}")
print(f"tower_c: {tower_c}")
    
hanoi_list(tower_a, tower_c, tower_b, num_discs) 

# 이동 후
print("\n이동 후:")
print(f"tower_a: {tower_a}")
print(f"tower_b: {tower_b}")
print(f"tower_c: {tower_c}")

시작할 때:
tower_a: [3, 2, 1]
tower_b: []
tower_c: []

이동 후:
tower_a: []
tower_b: []
tower_c: [3, 2, 1]

해결책 3

• 말뚝 구현을 위해 스택 자료구조 직접 활용 가능.
• 스택 클래스를 직접 선언함. 다음 두 가지 메서드 구현해야 함.
  • push(): 항목 추가를 위한 메서드
  • pop(): 항목 삭제를 위한 메서드

class Stack():
    def __init__(self):
        self._container = []

    def push(self, item):
        self._container.append(item)

    def pop(self):
        return self._container.pop()

    def __repr__(self):
        return repr(self._container)

def hanoi(begin, end, temp, n):
    if n == 1: 
        end.push(begin.pop())
    else:
        hanoi(begin, temp, end, n - 1) 
        hanoi(begin, end, temp, 1) 
        hanoi(temp, end, begin, n - 1)

tower_a = Stack() 
tower_b = Stack() 
tower_c = Stack()

# 디스크 수
num_discs = 5

for i in range(num_discs, 0, -1):
    tower_a.push(i)

# 시작할 때
print("시작할 때:")
print(f"tower_a: {tower_a}")
print(f"tower_b: {tower_b}")
print(f"tower_c: {tower_c}")
    
hanoi(tower_a, tower_c, tower_b, num_discs) 

# 이동 후
print("\n이동 후:")
print(f"tower_a: {tower_a}")
print(f"tower_b: {tower_b}")
print(f"tower_c: {tower_c}")

시작할 때:
tower_a: [5, 4, 3, 2, 1]
tower_b: []
tower_c: []

이동 후:
tower_a: []
tower_b: []
tower_c: [5, 4, 3, 2, 1]

• 참조: PythonTutor: 하노이탑 실행 과정