2장 분할정복¶
주요 내용¶
1편¶
- 1절 이분검색
- 2절 합병정렬
- 3절 분할정복 설계방법
2편¶
- 4절 퀵정렬(분할교환정렬)
- 5절 슈트라쎈의 행렬곱셈 알고리즘
- 8절 분할정복법을 사용할 수 없는 경우
1절 이분검색¶
- 분할정복은 재귀 알고리즘으로 쉽게 구현 가능
재귀 예제: 이분검색¶
문제: 항목이 비내림차순(오름차순)으로 정렬된 리스트 $S$에 $x$가 항목으로 포함되어 있는가?
입력 파라미터: 리스트 $S$와 값 $x$
리턴값:
- $x$가 $S$의 항목일 경우: $x$의 위치 인덱스
- 항목이 아닐 경우 -1.
복습: while 반복문을 활용한 이분검색¶
In [1]:
# 이분검색 알고리즘
def binsearch(S, x):
low, high = 0, len(S)-1
location = -1
# while 반복문 실행횟수 확인용
loop_count = 0
while low <= high and location == -1:
loop_count += 1
mid = (low + high)//2
if x == S[mid]:
location = mid
elif x < S[mid]:
high = mid - 1
else:
low = mid + 1
return (location, loop_count)
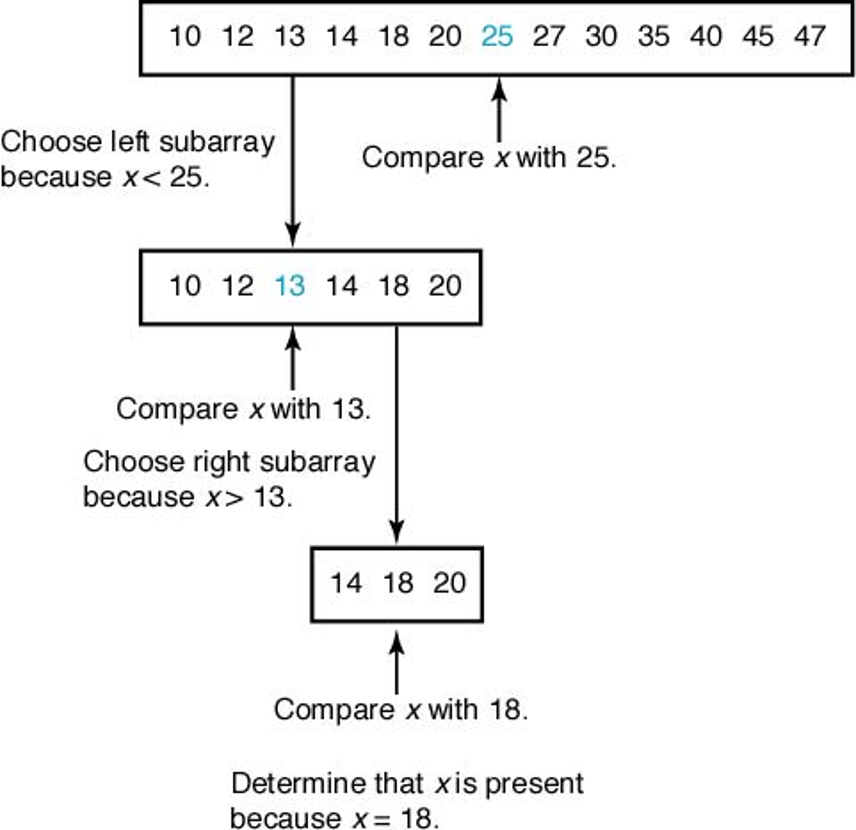
설계 전략¶
- $x$가 배열의 중앙에 위치하고 있는 항목과 같으면 해당 항목 인덱스 리턴.
- 그렇지 않으면 아래 실행
- 분할: 배열을 중앙에 위치한 항목을 기준으로 반으로 분할
- $x$가 중앙에 위치한 항목보다 작으면 왼쪽 배열 반쪽 선택
- 그렇지 않으면 오른쪽 배열 반쪽을 선택
- 정복: 선택된 반쪽 배열을 대상으로 1번 단계부터 다시 시작
- 분할: 배열을 중앙에 위치한 항목을 기준으로 반으로 분할
- 취합: 불필요!
재귀 이해¶
- "정복: 선택된 반쪽 배열을 대상으로 1번 단계부터 다시 시작" 이라는 표현이 재귀를 의미함.
- 분할정복으로 재귀 알고리즘을 개발할 때 아래 사항을 고려해야 함.
- 분할한 작은 입력사례의 답으로부터 전체 입력사례에 대한 답을 구하는 방법 고안
- 더 이상 분할이 불가능한 입력사례에 대한 판단할 종료조건 정하기
- 종료조건을 만족하는 경우 답을 구하는 방법 정하기
파이썬 구현: 이분검색 재귀¶
In [2]:
# 이분검색 재귀
def location(S,x, low, high):
if low > high:
return -1
mid = (low + high)//2
if x == S[mid]:
return mid
elif x < S[mid]:
return location(S, x, low, mid-1)
else:
return location(S, x, mid+1, high)
In [3]:
sec = [10, 12, 13, 14, 18, 20, 25, 27, 30, 35, 40, 45, 47]
x = 18
print(location(sec, x, 0, len(sec)-1))
주의사항¶
- 책 설명과는 달리
location함수의 인자로S와x를 추가하였음. - 이유:
location함수를 임의의 리스트와 임의의 값에 대해 사용하기 위해서. - 책에서
S와x를 인자로 사용하지 않은 이유:location함수를 재귀로 호출할 때마다S와x의 값이 매번 새롭게 할당되어 메모리가 많이 사용됨.
- 하지만 파이썬의 경우 기존의 리스트를 가리키는 변수를 재활용 함.
최악 시간복잡도 분석: 이분검색 재귀¶
- 입력크기: 리스트 길이
- 단위연산:
x와S[mid]비교
$n = 2^k$인 경우¶
아래 점화식 성립
\begin{align*} W(n) &= W \Big(\frac n 2 \Big) + 1 \quad \text{if }\, n>1\\ W(1) &= 1 \end{align*}
위 점화식에 대한 해답:
$$W(n) = \lg n + 1$$
점화식 해답 설명
\begin{align*} W(1) &= 1 \\ W(2) &= W(1) + 1 = 2 \\ W(2^2) &= W(2) + 1 = 3 \\ W(2^3) &= W(2^2) + 1 = 4 \\ ... & \\ W(2^k) &= W(2^{k-1}) + 1 = k+1 = \lg (2^k) + 1\\ \end{align*}
일반적인 경우¶
아래 최악 시간복잡도 성립
\begin{align*} W(n) &= \lfloor \lg n \rfloor + 1 \in \Theta(\lg n) \end{align*}
증명: 생략
2절 합병정렬¶
문제: 리스트의 항목을 비내림차순(오름차순)으로 정렬하기
입력 파라미터: 리스트 $S$
리턴값: $S$의 모든 항목을 크기순으로 포함한 리스트
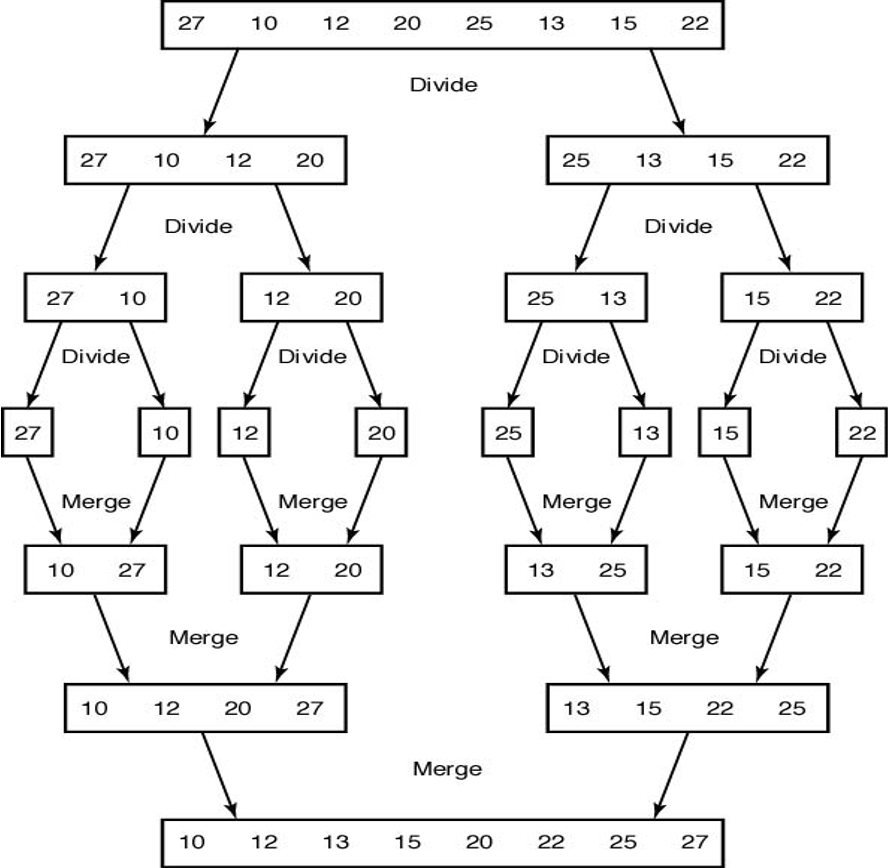
설계 전략¶
- 분할: 배열을 반으로 분할
- 정복: 분할된 왼쪽/오른쪽 배열을 대상으로 다음 실행
- 배열의 크기가 2 이상이면 1번 분할 단계로 이동
- 두 배열의 크기가 1이면 3번 통합 단계로 이동
- 통합: 정렬된 두 배열을 합병정렬 후 아직 정복되지 않은 배열이 남아 있는 경우 2번 정복 단계로 이동
파이썬 구현: 합병정렬 재귀¶
정렬된 두 리스트를 정렬된 리스트로 합병하기¶
- 입력값: 정렬된 두 리스트
- 리턴값: 두 리스트의 항목을 비내림차순으로 정렬한 리스트
예제: 작동법 설명¶
| 비교횟수 | left | right | 합병결과 |
|---|---|---|---|
| 1 | 10 12 20 27 | 13 15 22 25 | 10 |
| 2 | 10 12 20 27 | 13 15 22 25 | 10 12 |
| 3 | 10 12 20 27 | 13 15 22 25 | 10 12 13 |
| 4 | 10 12 20 27 | 13 15 22 25 | 10 12 13 15 |
| 5 | 10 12 20 27 | 13 15 22 25 | 10 12 13 15 20 |
| 6 | 10 12 20 27 | 13 15 22 25 | 10 12 13 15 20 22 |
| 7 | 10 12 20 27 | 13 15 22 25 | 10 12 13 15 20 22 25 |
| 10 12 20 27 | 13 15 22 25 | 10 12 13 15 20 22 25 27 |
In [4]:
# 정렬된 두 리스트를 정렬된 리스트로 합병하기
def merge(lList, rList):
mergedList =[]
while len(lList)>0 and len(rList)>0:
if lList[0] < rList[0]:
mergedList.append(lList.pop(0))
else:
mergedList.append(rList.pop(0))
mergedList.extend(lList)
mergedList.extend(rList)
return mergedList
In [5]:
a = [10, 12, 20, 27]
b = [13, 15, 22, 25]
merge(a, b)
Out[5]:
In [6]:
# 합병정렬 재귀
def mergesort(aList):
if len(aList) <= 1:
return aList
mid = len(aList) // 2
lList = mergesort(aList[:mid])
rList = mergesort(aList[mid:])
return merge(lList, rList)
In [7]:
aList = [27, 10, 12, 20, 25, 13, 15, 22]
mergesort(aList)
Out[7]:
최악 시간복잡도 분석: 합병(merge) 알고리즘¶
- 입력크기: 리스트 길이
- 단위연산: 비교연산
최악의 경우 예제:¶
- 오른쪽 리스트의 마지막 원소를 제외한 나머지를 먼저 옮긴다.
- 왼쪽 리스트의 모든 원소를 옮긴다.
- 오른쪽 마지막 원소를 옮긴다.
In [8]:
def merge_count(lList, rList):
mergedList =[]
count = 0
while len(lList)>0 and len(rList)>0:
count += 1
if lList[0] < rList[0]:
mergedList.append(lList.pop(0))
else:
mergedList.append(rList.pop(0))
mergedList.extend(lList)
mergedList.extend(rList)
print(f"count: {count}")
return mergedList
In [9]:
a1 = [18, 20, 23, 26]
b1 = [13, 15, 17, 27]
merge_count(a1, b1)
Out[9]:
최선의 경우 예제:¶
- 왼쪽 리스트 모든 항목이 오른쪽 리스트의 항목보다 작은 경우
In [10]:
a = [10, 12, 16, 18]
b = [19, 20, 22, 27]
merge_count(a, b)
Out[10]:
최악 시간복잡도 분석: 합병정렬(mergesort) 알고리즘¶
- 입력크기: 리스트 길이
- 단위연산:
merge함수에서 발생하는 비교연산
$n = 2^k$인 경우¶
- 아래 점화식 성립: $n > 1$ 인 경우
종료 조건:
$$W(1) = 0$$
위 점화식에 대한 해답:
$$W(n) = n\, \lg n - (n- 1) \in \Theta(n\, \lg n)$$
- 증명: 생략
일반적인 경우¶
아래 점화식 성립:
\begin{align*} W(n) &= W \Big(\Big\lfloor \frac n 2 \Big\rfloor\Big) + W \Big(\Big\lceil\frac n 2 \Big\rceil\Big) + (n-1) \end{align*}
따라서 다음 최악 시간복잡도 성립
\begin{align*} W(n) &\in \Theta(n\,\lg n) \end{align*}
- 증명: 생략
제자리 합병정렬¶
- 앞서 살펴본
mergesort()함수는 호출될 때마다 매번aList인자에 대한 메모리를 새롭게 사용.
이유: 파이썬 리스트의 슬라이싱을 사용하기 때문
lList = mergesort(aList[:mid]) rList = mergesort(aList[mid:])
- 재귀 함수를 호출할 때 추가 메모리를 사용하지 않는 방법
low와high를 추가 인자로 사용하여 주어진 리스트에서 살펴볼 구간을 가리키도록 함.
- 이런 합병정렬 알고리즘을 제자리 합병정렬이라 부름.
In [11]:
# 제자리 합병정렬 재귀
def mergesort2(aList, low, high):
if (low < high):
mid = (low + high) // 2
lList = mergesort2(aList, low, mid)
rList = mergesort2(aList, mid+1, high)
return merge(lList, rList)
return aList[low:low+1]
In [12]:
aList = [27, 10, 12, 20, 25, 13, 15, 22]
print(mergesort2(aList, 0, 7))
mergesort 와 mergesort2 공간복잡도¶
- 두 알고리즘의 시간 복잡도는 동일하지만 공간복잡도는 크게 차이남.
mergesort의 추가 메모리 공간복잡도¶
merge를 재귀호출할 때마다 입력 리스트만큼 메모리 추가 사용- 따라서
merge의 최악 시간복잡도만큼 추가 메모리 사용 - 즉,
mergesort알고리즘의 추가 메모리 일정 공간복잡도는 $\Theta(n \lg n)$
mergesort2의 추가 메모리 공간 복잡도¶
- 재귀 호출할 때 추가 메모리를 사용하지 않음.
- 즉, 추가 메모리에 대한 일정 공간복잡도는 상수. 즉, $\Theta(1)$.
mergesort 와 mergesort2의 실행시간 비교¶
- 실행시간 거의 차이 없음. 즉, 공간복잡도의 차이가 실행시간에 크게 영향 미치지는 않음.
merge함수를 실행할 때 드는 비용이 절대적이기 때문.
In [13]:
# 시간 측정을 위한 모듈
import time
In [14]:
bigNum = 1000000
reversedList = list(range(bigNum, 0, -1))
start_time = time.time()
mergesort(reversedList)
end_time = time.time()
duration = end_time - start_time
print(f"걸린시간: {duration:.2f}초")
In [15]:
bigNum = 1000000
reversedList = list(range(bigNum, 0, -1))
start_time = time.time()
mergesort2(reversedList, 0, bigNum)
end_time = time.time()
duration = end_time - start_time
print(f"걸린시간: {duration:.2f}초")
3절 분할정복 전략¶
- 분할(Divide)
- 입력사례를 여러 개의 보다 작은 입력 사례로 분할한다.
- 정복(Conquer: 해결)
- 각각의 보다 작은 입력사례에 대한 문제를 해결한다.
- 입력사례가 충분히 작지 않으면 분할 과정으로 돌아간다.
- (필요한 경우) 취합
- 보다 작은 입력사례에 대한 해답을 취합하여 원래 문제에 대한 해답을 구한다.