4절 차수¶
- 아래 두 알고리즘 중에서 어떤 알고리즘 선택?
- 알고리즘 A의 시간 복잡도: $100n$
- 알고리즘 B의 시간 복잡도: $0.01 n^2$
- $0.01 n^2$과 $100n$ 중에 누구의 복잡도가 더 커보임?
- 정답: $n$의 크기에 따라 달라짐.
- $n \le 10,000$: 알고리즘 B 선택
- $n > 10,000$: 알고리즘 A 선택
- 이유:
"궁극적으로 더 빠름"¶
'$n>10,000$인 임의의 양의 정수 $n$에 대해 $0.01 n^2$이 $100 n$ 보다 크다'를 다르게 표현하면 다음과 같음.
- $0.01 n^2$이 $100 n$ 보다 궁극적으로 크다
다음 성질을 갖는 정수 $N \ge 0$이 존재할 때 $f(n)$이 $g(n)$ 보다 궁극적으로 크다 라고 말함:
- $n>N$인 임의의 양의 정수 $n$에 대해 $f(n) > g(n)$.
시간 복잡도의 기준으로 볼 경우:
- $g(n)$이 $f(n)$ 보다 궁극적으로 빠르다 $\quad\Longleftrightarrow\quad$ $f(n)$이 $g(n)$ 보다 궁극적으로 크다
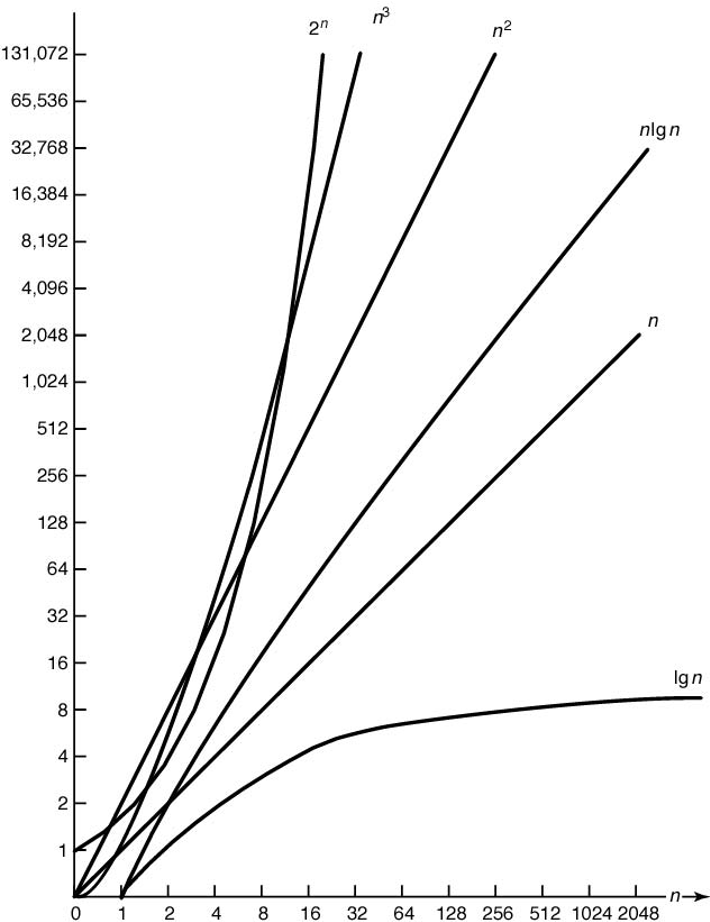
차수($\Theta$, 쎄타)의 직관적 이해¶
$\Theta(n)$: 1차 시간 복잡도¶
$$100 n, \quad 0.001 n+100, \quad \dots$$$\Theta(n^2)$: 2차 시간 복잡도¶
$$5 n^2, \quad 0.1 n^2 + n + 100, \quad \dots$$$\Theta(n^3)$: 3차 시간 복잡도¶
$$7 n^3, \quad n^3 + 5 n^2 + 100 n + 2, \quad \dots$$고차항의 지배력¶
- 예제: $0.1 n^2 + n + 100$에서 2차 항 $0.1 n^2$이 함수 전체를 지배함
| $n$ | $0.1 n^2$ |
$0.1 n^2 + n + 100$ |
|---|---|---|
| 10 | 10 | 120 |
| 20 | 40 | 160 |
| 50 | 250 | 400 |
| 100 | 1,000 | 1,200 |
| 1,000 | 100,000 | 101,100 |
복잡도 카테고리의 직관적 이해¶
- 1차, 2차, 3차 등의 시간복잡도를 갖는 함수들의 집합을 복잡도 카테고리라고 함.
매우 효율적인 알고리즘의 복잡도 예제¶
$\Theta(1)$: 상수 복잡도¶
$$1, \quad 17, \quad 1000, \quad 1000000, \quad \dots$$$\Theta(\lg n)$: 로그 복잡도¶
$$\lg n, \quad 2 \lg n, \quad \frac{1}{2} \cdot \lg n+ 3, \quad \dots$$$\Theta(n)$: 1차 복잡도¶
$$n, \quad 100 n, \quad 0.001 n + 10000, \quad \dots$$$\Theta(n\, \lg n)$: 엔 로그 엔(n log n) 복잡도¶
$$n\, \lg n, \quad 2 n\, \lg n, \quad \frac 1 2 n\, \lg n+ \lg n + 3, \quad \dots$$경우에 따라 괜찮은 알고리즘의 복잡도 예제¶
$\Theta(n^2)$: 2차 복잡도¶
$$n^2, \quad 5 n^2, \quad 0.1 n^2 + n + 100, \quad \dots$$$\Theta(n^3)$: 3차 복잡도¶
$$n^3, \quad 0.001 n^3 + 5 n^2 + 2 n + 7, \quad 100 n^3 + n + 100, \quad \dots$$사실상 사용할 수 없는 알고리즘의 복잡도 예제¶
$\Theta(2^n)$: 지수 복잡도¶
$$2^n, \quad 0.001\cdot 2^n + 5 n^3 + 2 n + 7, \quad 3\cdot 2^n + 100 n^3 + n + 100, \quad \dots$$$\Theta(n!)$: 팩토리얼 복잡도¶
$$n!, \quad 2\cdot n! + 5\cdot 2^n + 5 n^3 + 2 n + 7, \quad 0.01 n! + 3\cdot 2^n + 100 n^3 + n + 100, \quad \dots$$시간복잡도별 실행시간 비교¶
- 가정: 단위연산 실행시간 = 1 ns
$n$ |
$\lg n$ |
$n$ |
$n\, \lg n$ |
$n^2$ |
$n^3$ |
$2^n$ |
|---|---|---|---|---|---|---|
| $10$ | $0.003$ $\mu$s | $0.01$ $\mu$s | $0.033$ $\mu$s | $0.10$ $\mu$s | $1.0$ $\mu$s | $1$ $\mu$s |
| $20$ | $0.004$ $\mu$s | $0.02$ $\mu$s | $0.086$ $\mu$s | $0.40$ $\mu$s | $8.0$ $\mu$s | $1$ ms |
| $30$ | $0.005$ $\mu$s | $0.03$ $\mu$s | $0.147$ $\mu$s | $0.90$ $\mu$s | $27.0$ $\mu$s | $1$ 초 |
| $40$ | $0.005$ $\mu$s | $0.04$ $\mu$s | $0.213$ $\mu$s | $1.60$ $\mu$s | $64.0$ $\mu$s | $18.3$ 분 |
| $50$ | $0.006$ $\mu$s | $0.05$ $\mu$s | $0.282$ $\mu$s | $2.50$ $\mu$s | $125.0$ $\mu$s | $13$ 일 |
| $10^2$ | $0.007$ $\mu$s | $0.10$ $\mu$s | $0.664$ $\mu$s | $10.00$ $\mu$s | $1.0$ ms | $4 \times 10^{13}$ 년 |
$n$ |
$\lg n$ |
$n$ |
$n\, \lg n$ |
$n^2$ |
$n^3$ |
$2^n$ |
|---|---|---|---|---|---|---|
| $10^3$ | $0.010$ $\mu$s | $1.00$ $\mu$s | $9.966$ $\mu$s | $1.00$ ms | $1.0$ 초 | |
| $10^4$ | $0.013$ $\mu$s | $10.00$ $\mu$s | $130.000$ $\mu$s | $100.00$ ms | $16.7$ 분 | |
| $10^5$ | $0.017$ $\mu$s | $0.10$ ms | $1.670$ ms | $10.00$ 초 | $11.6$ 일 | |
| $10^6$ | $0.020$ $\mu$s | $1.00$ ms | $19.930$ ms | $16.70$ 초 | $31.7$ 년 | |
| $10^7$ | $0.023$ $\mu$s | $0.01$ 초 | $0.230$ 초 | $1.16$ 일 | $31,709$ 년 | |
| $10^8$ | $0.027$ $\mu$s | $0.10$ 초 | $2.660$ 초 | $115.70$ 일 | $3.17 \times 10^7$ 년 | |
| $10^9$ | $0.030$ $\mu$s | $1.00$ 초 | $29.900$ 초 | $31.70$ 년 |
- 원서 오류 주의: 약 $0.230$ 초
차수 정의¶
- 차수($\Theta$)를 엄밀하게 정의하려면 "큰 $O$(big $O$)"와 "$\Omega$(Omega, 오메가)" 개념 필요
'큰 $O$' 표기법¶
다음 성질을 갖는 양의 실수 $c$와 음이 아닌 정수 $N$이 존재할 때 $g(n)\in O(f(n))$ 성립:
- $n \ge N$인 임의의 정수 $n$에 대해 $g(n) \le c\cdot f(n)$
$g(n) \in O(f(n))$ 읽는 방법:
$g(n)$은 $f(n)$의 큰 $O$이다.
$g(n)$의 점근적 상한은 $f(n)$이다.
- 의미: 입력크기 $n$에 대해 시간 복잡도 $g(n)$의 수행시간은 궁극적으로 $f(n)$보다 나쁘지는 않다.
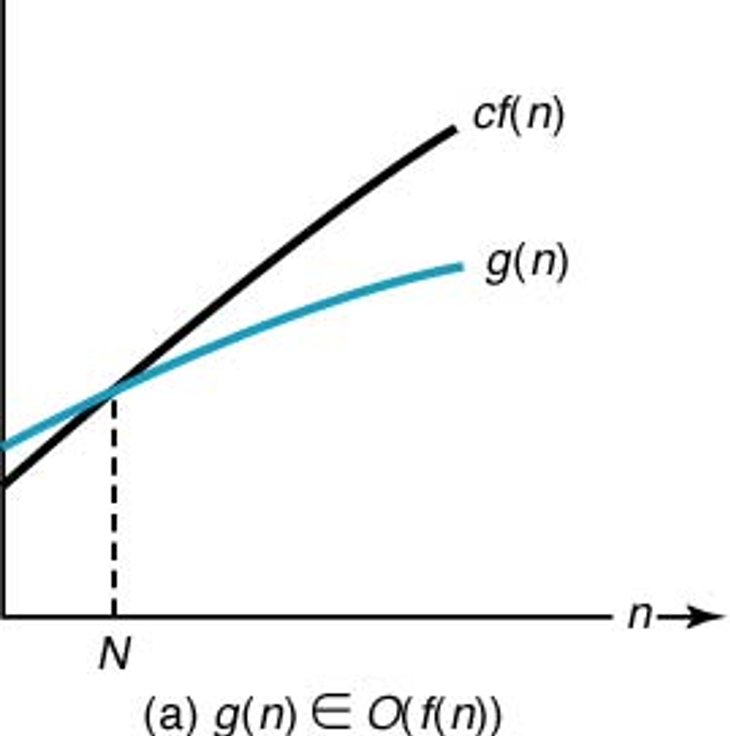
'큰 $O$' 표기법 예제¶
$n^2+10n \in O(n^2)$
$n \ge 10$인 경우: $$n^2+10n \le 2n^2$$
그러므로 $c=2$와 $N=10$ 선택
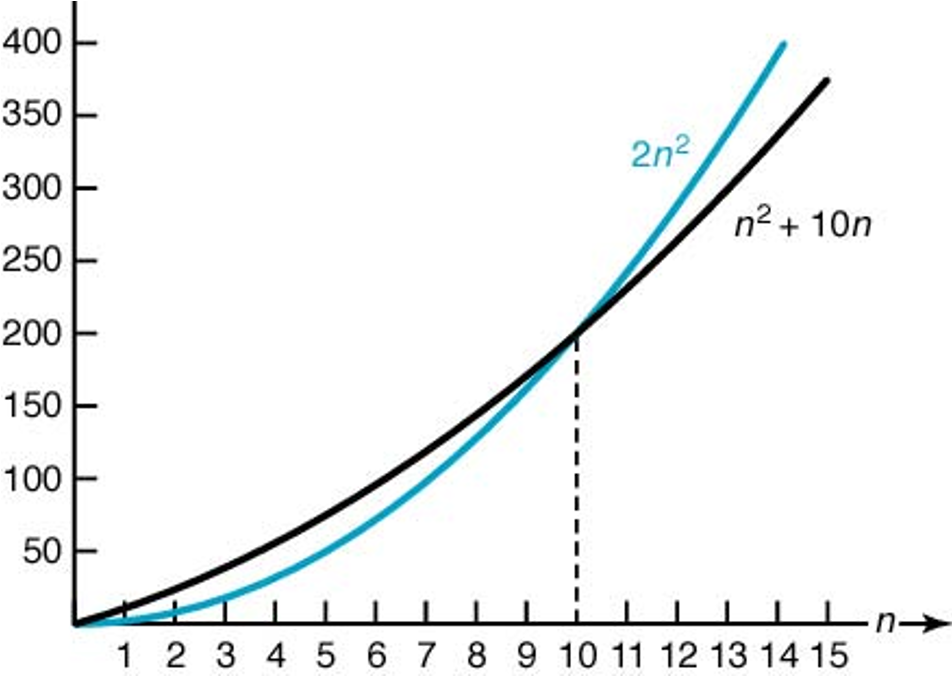
$5n^2 \in O(n^2)$
$n\ge 0$인 경우:
$$5n^2 \le 5n^2$$
그러므로 $c=5$와 $N=0$ 선택
$\frac{n(n-1)}{2} \in O(n^2)$
$n \ge 0$인 경우:
$$n(n-1)/2 \le \frac{n^2}{2}$$
그러므로 $c = 1/2$과 $N=0$ 선택
$n^2 \in O(n^2+10n)$
$n \ge 0$인 경우:
$$n^2 \le 1 \times (n^2+10n)$$
그러므로 $c=1$과 $N=0$ 선택
$n \in O(n^2)$
$n \ge 1$인 경우:
$$n \le 1 \times n^2$$
그러므로 $c=1$과 $N=1$ 선택
$n^3 \not\in O(n^2)$
$c$와 $N$을 아무리 크게 지정하더라도, $N$ 보다 큰 어떤 수 $n$에 대해 다음이 성립:
$$n^3 > c\cdot n^2$$
예를 들어, $n > c$로 잡으면 됨.
- $O(n^2)$: 특정 양의 실수 $c$에 대해 $c\, n^2$ 보다 궁극적으로 작은 값을 가지는 함수들의 집합
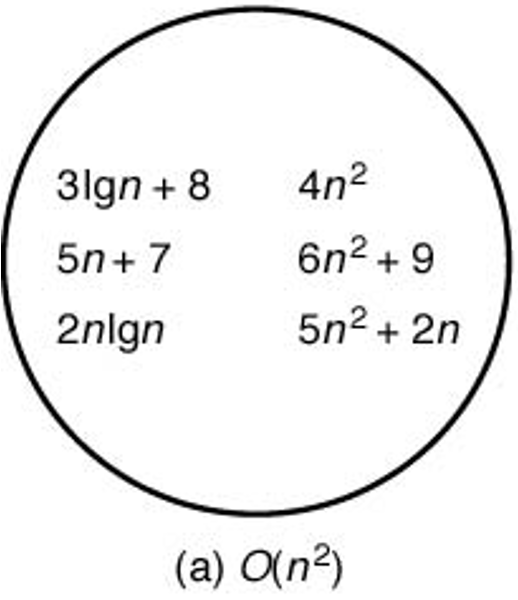
$\Omega$ 표기법¶
다음 성질을 갖는 양의 실수 $c$와 음이 아닌 정수 $N$이 존재할 때 $g(n)\in \Omega(f(n))$ 성립:
- $n \ge N$인 임의의 정수 $n$에 대해 $g(n) \ge c\cdot f(n)$
$g(n) \in \Omega(f(n))$ 읽는 방법:
$g(n)$은 $f(n)$의 오메가이다.
$g(n)$의 점근적 하한은 $f(n)$이다.
- 의미: 입력크기 $n$에 대해 시간 복잡도 $g(n)$의 수행시간은 궁극적으로 $f(n)$보다 효율적이지 못하다.
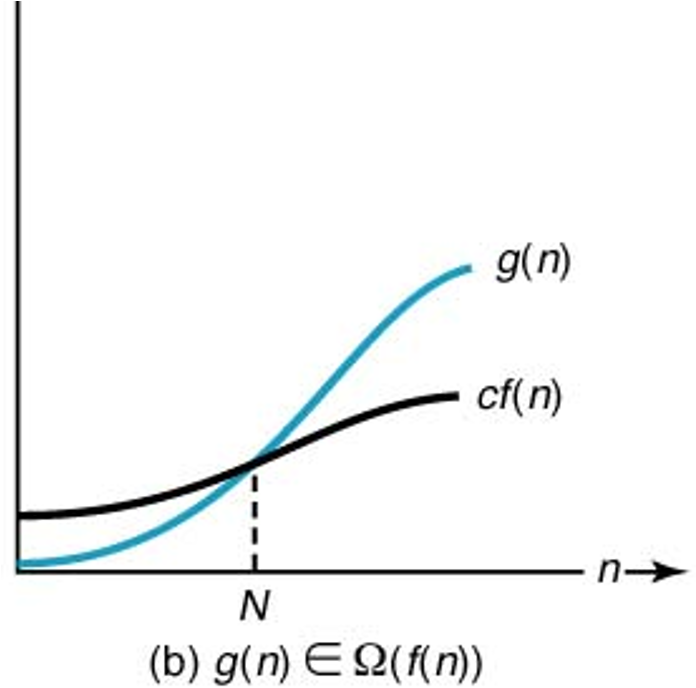
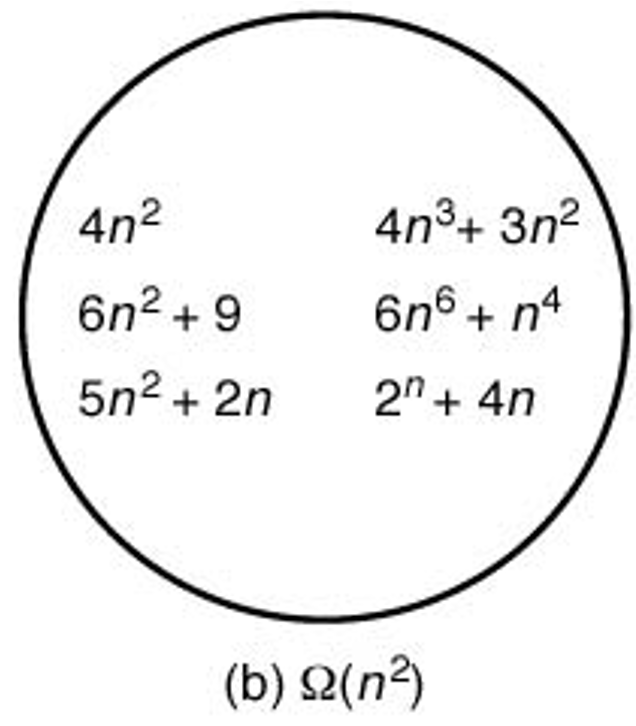
$\Omega$ 표기법 예제¶
$n^2 + 10n \in \Omega(n^2)$
$n \ge 0$인 경우:
$$n^2+10n \ge n^2$$
그러므로 $c = 1$과 $N = 0$ 선택
$5n^2 \in \Omega(n^2)$
$n \ge 0$인 경우:
$$5n^2 \ge 1\cdot n^2$$
그러므로, $c=1$과 $N=0$ 선택
$\frac{n(n-1)}{2} \in \Omega(n^2)$
$n \ge 2$인 경우:
$$\frac{n(n-1)}{2} \ge \frac{1}{4} n^2$$
그러므로 $c = 1/4$과 $N = 2$ 선택
$n^3 \in \Omega(n^2)$
$n \ge 1$인 경우:
$$n^3 \ge 1 \cdot n^2$$
그러므로, $c = 1$과 $N = 1$ 선택
$n \not\in \Omega(n^2)$
$c$를 아무리 작게, $N$을 아무리 크게 지정하더라도, $n \le c\cdot n^2$을 만족시키는 $n\ge N$이 존재.
예를 들어, $n \ge 1/c$로 잡으면 됨.
- $\Omega(n^2)$: 특정 양의 실수 $c$에 대해 $c\, n^2$ 보다 궁극적으로 큰 값을 가지는 함수들의 집합
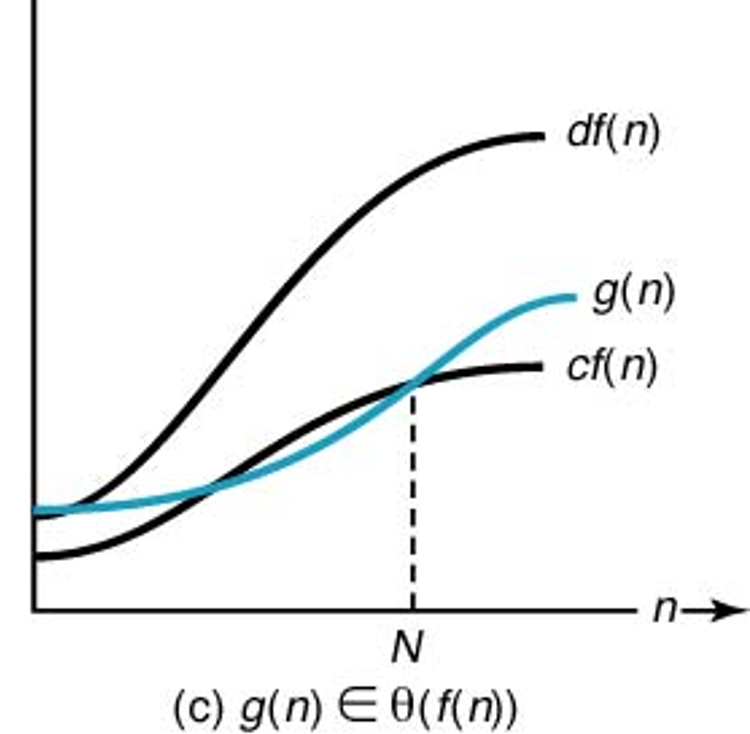
$\Theta$ 표기법¶
즉, 다음 성질을 갖는 양의 실수 $c$와 $d$, 그리고 음이 아닌 정수 $N$이 존재할 때 $g(n)\in \Theta(f(n))$ 성립:
- $n \ge N$인 임의의 정수 $n$에 대해 $c\cdot f(n) \le g(n) \le d\cdot f(n)$
$g(n) \in \Theta(f(n))$ 읽는 방법:
- $g(n)$의 $f(n)$의 차수이다.
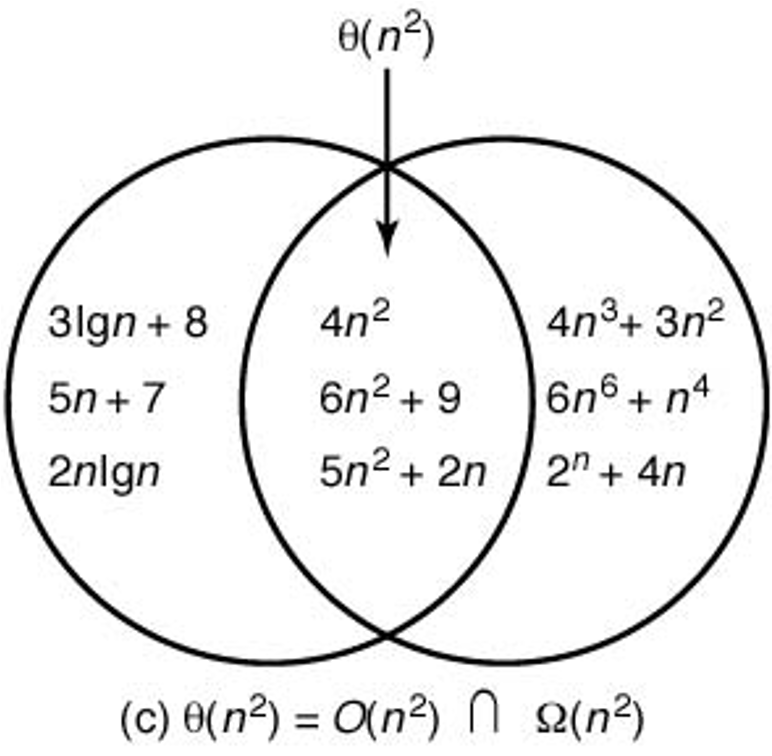
$\Theta$ 표기법 예제¶
$\frac{n (n-1)}{2} \in \Theta(n^2)$:
$n\ge 2$인 경우:
$$\frac{n (n-1)}{2} \ge \frac 1 4 n^2$$
$n \ge 0$인 경우:
$$\frac{n (n-1)}{2} \le \frac 1 2 n^2$$
그러므로, $c = \frac 1 4$, $d = \frac 1 2$, $N = 2$.
작은 $o$(small $o$) 표기법¶
임의의 양의 실수 $c$에 대해 다음 성질을 갖는 음이 아닌 정수 $N$이 존재할 때 $g(n)\in o(f(n))$ 성립:
- $n \ge N$인 임의의 정수 $n$에 대해 $g(n) \le c\cdot f(n)$
$g(n) \in o(f(n))$ 읽는 방법:
- $g(n)$은 $f(n)$의 '작은 오(small $o$)이다.
의미
$g(n)$이 $f(n)$에 비해 궁극적으로 하찮을 만큼 작다.
알고리즘 분석적 측면: 복잡도 $g(n)$이 복잡도 $f(n)$ 보다 궁극적으로 훨씬 좋다.
- 이유: $c>0$이 아무리 작더라도, $n$이 충분히 크면 $g(n) < f(n)$ 성립하기 때문.
큰 $O$ vs 작은 $o$¶
큰 $O$: 하나의 양의 실수 $c$에 대해서 부등식 성립
작은 $o$: 모든 양의 실수 $c$에 대해서 부등식 성립
작은 $o$ 표기법 예제¶
$n \in o(n^2)$
- $c > 0$가 주어졌을 때, $n \ge 1/c$ 인 모든 $n$에 대해 $n \le c\cdot n^2$ 성립.
$n \not\in o(5n)$
- $c < 1/5$인 경우, 임의의 음이 아닌 정수 $n$에 대해 $n > c\cdot 5n$ 성립.
$n^2 \not\in o(5n)$
이유:
$$n \not\in o(5n)$$
작은 $o$ 특성¶
가정:
$$g(n) \in o(f(n))$$
다음 성립:
$$ g(n) \in O(f(n)) - \Omega(f(n)) $$
증명: 생략.
주의사항¶
- $o(f(n)) \neq O(f(n)) - \Omega(f(n))$
- 다음 함수 $g(n)$에 대해 $g(n) \in O(n) - \Omega(n)$이지만 $g(n) \not\in o(n)$임:
차수의 특성¶
- $g(n) \in O(f(n)) \quad\Longleftrightarrow\quad f(n) \in \Omega(g(n))$
- $g(n) \in \Theta(f(n)) \quad\Longleftrightarrow\quad f(n) \in \Theta(g(n))$
임의의 $a, b > 1$에 대해
$$\log_a n \in \Theta(\log_b n)$$
즉, 로그 함수는 모두 동일한 복잡도 카테고리에 속함.
$b > a > 0$이면 다음 성립:
$$a^n \in o(b^n)$$
즉, 지수 함수는 밑수가 다르면 다른 복잡도 카테고리에 속함.
임의의 양의 실수 $a$에 대해 다음 성립:
$$a^n \in o(n!)$$
즉, $n!$은 어떠한 지수 복잡도함수보다 더 나쁘다(느리다).
많이 언급되는 복잡도 카테고리를 순서대로 나열하면 다음과 같음:
$$\Theta(\lg n)\;\; \Theta(n)\;\; \Theta(n\, \lg n)\;\; \Theta(n^2)\;\; \Theta(n^j)\;\; \Theta(n^k)\;\; \Theta(a^n)\;\; \Theta(b^n)\;\; \Theta(n!)$$
단, $k > j > 2$이고 $b > a > 1$임.
$g(n)$이 $f(n)$의 카테고리 보다 왼편에 위치한 카테고리에 속한 경우 다음 성립:
$$g(n) \in o(f(n))$$
$c\ge 0$, $d>0$, $g(n) \in O(f(n))$, $h(n) \in \Theta(f(n))$ 인 경우 다음 성립:
$$c \cdot g(n) + d\cdot h(n) \in \Theta(f(n))$$
예제¶
$$\Theta(\log_4 n) \in \Theta(\lg n)$$극한(limit)을 이용하여 차수를 구하는 방법¶
정리¶
$\lim_{n\to \infty} \frac{g(n)}{f(n)}$의 값이
만약 $c > 0$이면, $g(n) \in \Theta(f(n))$,
만약 $0$ 이면, $g(n) \in o(f(n))$,
만약 $\infty$, 즉, 발산하면, $f(n) \in o(g(n))$.
예제¶
- $\frac{n^2}{2} \in o(n^3)$
- 만약 $b>a>0$이면 다음이 성립:
- 이유
$a>0$일 때, $a^n \in o(n!)$
- 증명 생략.
로피탈(L'Hopital)의 법칙¶
아래 조건이 성립한다고 가정하자.
$$\lim_{n\to \infty} f(n) = \lim_{n\to \infty} g(n) = \infty$$그러면 다음이 성립한다.
$$\lim_{n\to \infty} \frac{g(n)}{f(n)} = \lim_{n\to \infty} \frac{g'(n)}{f'(n)}$$예제¶
- 다음이 성립한다.
- 이유
예제¶
- 다음이 성립한다.
- 이유