2절 효율적 알고리즘 개발 중요성¶
효율적 검색 알고리즘 예제: 이분검색¶
- 문제: 항목이 비내림차순(오름차순)으로 정렬된 리스트 $S$에 $x$가 항목으로 포함되어 있는가?
- 입력 파라미터: 리스트 $S$와 값 $x$
- 리턴값:
- $x$가 $S$의 항목일 경우: $x$의 위치 인덱스
- 항목이 아닐 경우 -1.
In [1]:
# 이분검색 알고리즘
def binsearch(S, x):
low, high = 0, len(S)-1
location = -1
# while 반복문 실행횟수 확인용
loop_count = 0
while low <= high and location == -1:
loop_count += 1
mid = (low + high)//2
if x == S[mid]:
location = mid
elif x < S[mid]:
high = mid - 1
else:
low = mid + 1
return (location, loop_count)
In [2]:
seq = list(range(30))
val = 5
print(binsearch(seq, val))
(5, 5)
In [3]:
seq = list(range(30))
val = 10
print(binsearch(seq, val))
(10, 3)
In [4]:
seq = list(range(30))
val = 20
print(binsearch(seq, val))
(20, 4)
In [5]:
seq = list(range(30))
val = 29
print(binsearch(seq, val))
(29, 5)
In [6]:
seq = list(range(30))
val = 30
print(binsearch(seq, val))
(-1, 5)
In [7]:
seq = list(range(30))
val = 100
print(binsearch(seq, val))
(-1, 5)
- 입력값이 달라져도
while반복문의 실행횟수가 거의 변하지 않음.
파이썬튜터 활용: 이분검색¶
- 위 이분검색 코드를 PythonTutor: 이분검색 에서 실행하면서 메모리에서의 변화 확인 가능
이분검색 분석¶
이분검색으로 특정 값의 위치를 확인하기 위해서 $S$의 항목 몇 개를 검색해야 하는가?
while반복문이 실행될 때마다 검색 대상의 총 크기가 절반으로 감소됨.- 따라서 최악의 경우 $(\lfloor\lg n\rfloor + 1)$개의 항목만 검사하면 됨.
- 여기서 $\lg := \log_2$.
순차검색 vs 이분검색¶
- 최악의 경우 확인 항목수
배열 크기 |
순차 검색 |
이분 검색 |
|---|---|---|
| $n$ | $n$ | $\lg n + 1$ |
| $128$ | $128$ | $8$ |
| $1,024$ | $1,024$ | $11$ |
| $1,048,576$ | $1,048,576$ | $21$ |
| $4,294,967,296$ | $4,294,967,296$ | $33$ |
이분검색 활용¶
- 다음, 네이버, 구글, 트위터 등등 수백에서 수천만의 회원을 대상으로 검색을 진행하고자 한다면 어떤 알고리즘 선택?
당연히 이분검색!
- 이분 검색은 검색 속도가 사실상 최고로 빠름
예제: 피보나찌 수 구하기 알고리즘¶
- 피보나치 수열 정의
- 피보나찌 수 예제
피보나찌 수 구하기 알고리즘(재귀)¶
- 문제: 피보나찌 수열에서 $n$번째 수를 구하라.
- 입력: 음이 아닌 정수
- 출력: $n$번째 피보나찌 수
In [8]:
# 피보나찌 수 구하기 알고리즘(재귀)
def fib(n):
if (n <= 1):
return n
else:
return fib(n-2) + fib(n-1)
In [9]:
fib(3)
Out[9]:
2
In [10]:
fib(6)
Out[10]:
8
In [11]:
fib(10)
Out[11]:
55
fib 함수 분석¶
- 작성하기도 이해하기도 쉽지만, 매우 비효율적임.
- 이유는 동일한 값을 반복적으로 계산하기 때문.
- 예를들어,
fib(5)를 계산하기 위해fib(2)가 세 번 호출됨. 아래 나무구조 그림 참조.
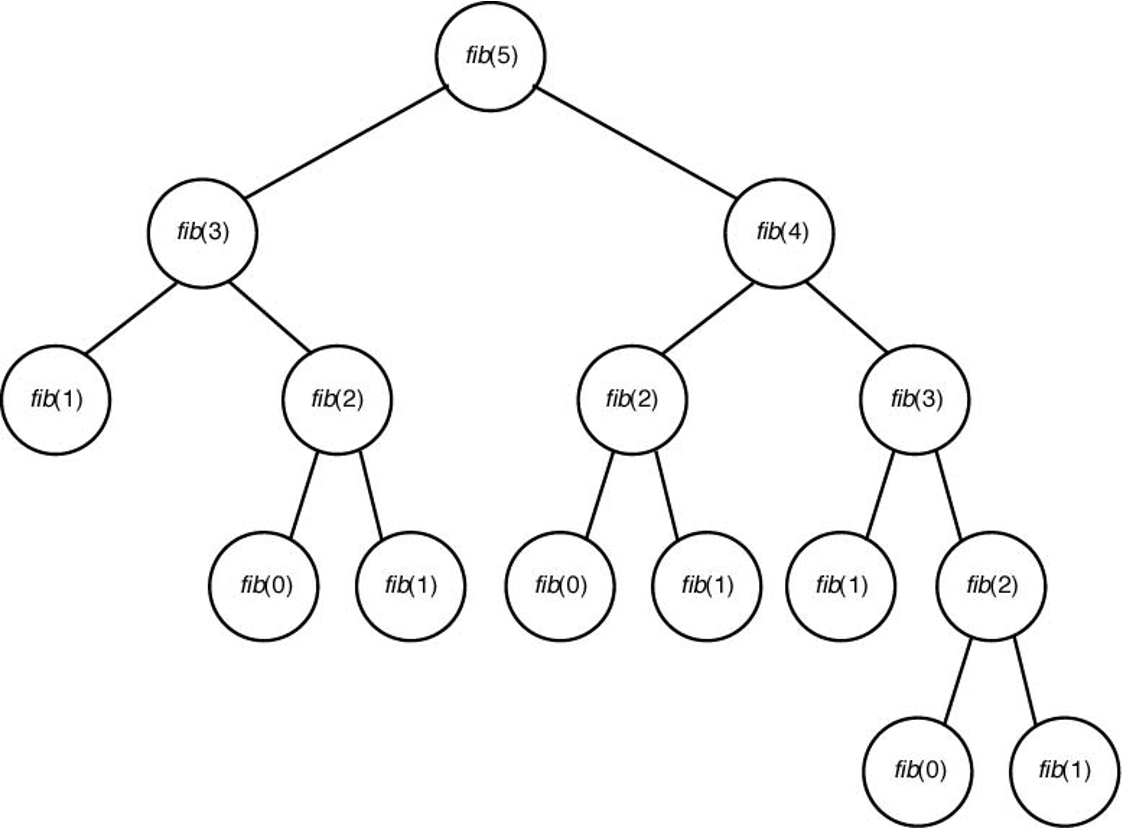
fib 함수 호출 횟수¶
- $T(n)$ =
fib(n)을 계산하기 위해fib함수를 호출한 횟수.- 즉,
fib(n)을 위한 재귀 나무구조에 포함된 마디(node)의 개수
- 즉,
- 아래 부등식 성립.
\begin{align*}
T(0) &= 1 \\
T(1) &= 1 \\
T(n) &= T(n - 1) + T(n - 2) +1 \quad (n \ge 2) \\
&> 2 \times T(n - 2) \qquad\qquad\quad\; (T(n - 1) > T(n - 2)) \\
&> 2^2 \times T(n - 4) \\
&> 2^3 \times T(n - 6) \\
& \dots \\
&> 2^{n/2} \times T(0) = 2^{n/2}
\end{align*}
피보나찌 수 구하기 알고리즘 (반복)¶
- 한 번 계산한 값을 리스트에 저장.
- 중복 계산 없음: 필요할 때 저장된 값 활용
- 하지만 입력크기에 비례하는 리스트 저장공간 활용
- 매우 비효율적인 메모리 활용으로 피보나찌 수 계산에 제한 받음.
In [12]:
# 피보나찌 수 구하기 알고리즘 (반복)
# 비효율적 메모리 활용
def fib2(n):
f = []
f.append(0)
if n > 0:
f.append(1)
for i in range(2, n+1):
fi = f[i-2] + f[i-1]
f.append(fi)
return f[n]
In [13]:
fib2(3)
Out[13]:
2
In [14]:
fib2(6)
Out[14]:
8
In [15]:
fib2(10)
Out[15]:
55
In [16]:
fib2(13)
Out[16]:
233
fib2(백만)계산 가능. 몇 분 걸림.
- 중복 계산이 없는 반복 알고리즘은 수행속도가 훨씬 더 빠름.
fib2 함수 분석¶
fib2함수 호출 횟수 $T(n)$- $T(n) = n + 1$
- 즉,
f[0]부터f[n]까지 한 번씩만 계산
두 피보나찌 알고리즘의 비교¶
- 가정: 피보나찌 수 하나를 계산하는 데 걸리는 시간 = 1 ns.
- 1 ns = $10^{-9}$ 초
- 1 $\mu$s = $10^{-6}$ 초
$n$ |
$n+1$ |
$2^{n/2}$ |
반복 |
재귀 |
|---|---|---|---|---|
| $40$ | $41$ | $1,048,576$ | $41$ ns | $1048$ $\mu$s |
| $60$ | $61$ | $1.1 \times 10^9$ | $61$ ns | $1$ 초 |
| $80$ | $81$ | $1.1 \times 10^{12}$ | $81$ ns | $18$ 분 |
| $100$ | $101$ | $1.1 \times 10^{15}$ | $101$ ns | $13$ 일 |
| $120$ | $121$ | $1.2 \times 10^{18}$ | $121$ ns | $36$ 년 |
| $160$ | $161$ | $1.2 \times 10^{24}$ | $161$ ns | $3.8 \times 10^7$ 년 |
| $200$ | $201$ | $1.3 \times 10^{30}$ | $201$ ns | $4 \times 10^{13}$ 년 |
피보나찌 수 구하기 알고리즘 (반복 버전 2)¶
- 한 번 계산한 값을 리스트에 저장.
- 중복 계산 없음: 필요할 때 저장된 값 활용
- 입력크기에 상관없이 길이가 2인 메모리 저장공간 활용
fib2함수보다 더 많은 피보나찌 수 계산 가능.
In [17]:
# 피보나찌 수 구하기 알고리즘 (반복)
# 효율적 메모리 활용
def fib3(n):
f = []
f.append(0)
if n > 0:
f.append(1)
for i in range(2, n+1):
fi = f[0] + f[1]
f[0], f[1] = f[1], fi
return f[1]
fib3(백만)계산 가능. 몇 초 걸림.fib2(백만)에 비해 백 배정도 빠름.- 천만번째 피보나찌 수? 글쎄...