1장 알고리즘: 효율성, 분석, 차수

책 소개

  • 알고리즘 기초(Foundations of Algorithms)
  • 리차드 네아폴리탄 저, 도경구 역, 홍릉과학출판사
  • 주요 내용: 컴퓨터로 문제 푸는 기법 배우기

목차

  • 1장: 알고리즘: 효율성, 분석, 차수
  • 2장 - 6장: 다양한 문제풀이 기법 및 적용 예제
    • 2장 분할정복
    • 3장 동적계획
    • 4장 탐욕 알고리즘
    • 5장 되추적
    • 6장 분기한정법
  • 7장 계산복잡도 소개: 정렬문제
  • 8장 계산복잡도: 검색문제
  • 9장 계산복잡도와 문제 난이도: NP 이론 소개

1장 주요 내용

  • 1절 알고리즘
  • 2절 효율적인 알고리즘 개발 중요성
  • 3절 알고리즘 분석
  • 4절 차수

1절 알고리즘

프로그램 설계 과정

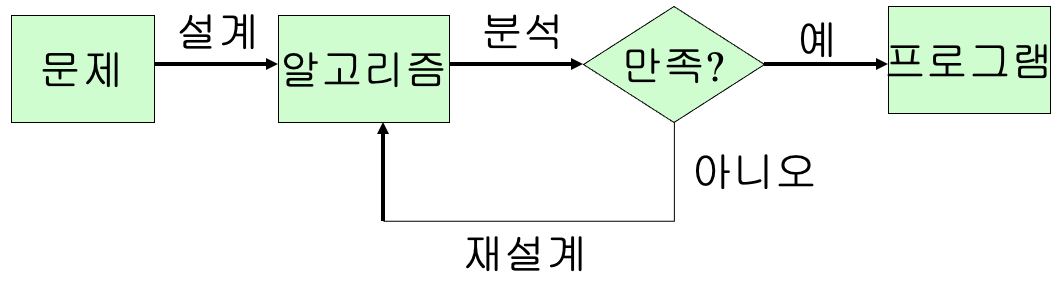
알고리즘이란?

  • 컴퓨터를 이용하여 주어진 문제를 해결하는 기법
  • 컴퓨터 프로그램은 여러 방법 중에서 한 가지 방법을 선택하여 구현
  • 프로그래밍 언어, 프로그래밍 스타일과 무관

알고리즘과 절차

  • 절차: 문제해결 알고리즘 적용 순서

알고리즘 효율성 분석

효율성

  • 문제해결을 위한 필수 요소
  • 컴퓨터 속도가 아무리 빨라져도, 메모리 가격이 아무리 저렴해져도 효율성 문제는 언제나 중요!
  • 수천년, 수만년 동안 실행되어야 끝나는 비효율적 알고리즘이 일반적으로 존재.

분석

  • 알고리즘의 효율성 판단
  • 효율성 판단 기준: 계산복잡도
  • 계산복잡도
    • 시간복잡도: 특정 연산의 실행 횟수
    • 공간복잡도: 메모리 공간 사용 정도

차수

  • 계산복잡도 판단 기준
  • 계산복잡도 함수의 차수(order) 기준
  • 차수를 이용하여 알고리즘을 계산복잡도를 기준으로 다양한 카테고리로 분류

알고리즘 효율성 비교 예제

  • 문제: 전화번호부에서 '홍길동'의 전화번호 찾기
  • 알고리즘 1: 순차검색
    • 첫 쪽부터 '홍길동'이라는 이름이 나올 때까지 순서대로 찾는다.
  • 알고리즘 2: 이분검색
    • 전화번호부는 '가나다'순
    • 먼저 'ㅎ'이 있을 만한 곳을 적당히 확인
    • 이후 앞뒤로 뒤적여가며 검색

분석: 어떤 알고리즘이 더 효율적인가?

  • 이분검색이 보다 효율적임.

알고리즘 표기법

  • 자연어: 한글 또는 영어
    • 단점 1: 복잡한 알고리즘 설명과 전달 어려움
    • 단점 2: 실제로 구현하기 어려움
  • 의사코드(Pseudo-code)
    • 실제 프로그래밍 언어와 유사한 언어로 작성된 코드
    • 자연어 사용의 단점 해결
    • 하지만 직접 실행할 수 없음.
    • 교재: C++에 가까운 의사코드 사용

강의에 사용되는 언어: 파이썬3

  • 설치: 아나콘다(Anaconda) 패키지 설치 추천
  • 주피터 노트북 활용
  • 파이썬은 기본패키지만 사용

파이썬 활용의 장점

  • 의사코드 수준의 프로그래밍 작성 가능
  • 책의 의사코드와 매우 유사하게 구현하여 실행 가능

예제: 순차검색

  • 문제: 리스트 $S$에 $x$가 항목으로 포함되어 있는가?
  • 입력 파라미터: 리스트 $S$와 값 $x$
  • 리턴값:
    • $x$가 $S$의 항목일 경우: $x$의 위치 인덱스
    • 항목이 아닐 경우 -1.
In [1]:
# 순차검색 알고리즘

def seqsearch(S, x):
    location = 0
    
    # while 반복문 실행횟수 확인용
    loop_count = 0

    while location < len(S) and S[location] != x:
        loop_count += 1
        location += 1

    if location < len(S):
        return (location, loop_count)
    else:
        return (-1, loop_count)
In [2]:
seq = list(range(30))
val = 5

print(seqsearch(seq, val))

(5, 5)
In [3]:
seq = list(range(30))
val = 10

print(seqsearch(seq, val))

(10, 10)
In [4]:
seq = list(range(30))
val = 20

print(seqsearch(seq, val))

(20, 20)
In [5]:
seq = list(range(30))
val = 29

print(seqsearch(seq, val))

(29, 29)
In [6]:
seq = list(range(30))
val = 30

print(seqsearch(seq, val))

(-1, 30)
In [7]:
seq = list(range(30))
val = 100

print(seqsearch(seq, val))

(-1, 30)
  • 입력값의 위치에 따라 while 반복문의 실행횟수가 선형적으로 달라짐.

파이썬튜터 활용: 순차검색

순차검색 분석

  • 특정 값의 위치를 확인하기 위해서 $S$의 항목 몇 개를 검색해야 하는가?
    • 특정 값과 동일한 항목의 위치에 따라 다름
    • 최악의 경우: $S$의 길이, 즉, 항목의 개수
  • 좀 더 빨리 찾을 수는 없는가?
    • $S$에 있는 항목에 대한 정보가 없는 한 더 빨리 찾을 수 없음.